In Section 11.3, we mention that a causal complex cepstrum x[n] is equivalent to the minimum-phase condition
Question:
In Section 11.3, we mention that a causal complex cepstrum x[n] is equivalent to the minimum-phase condition of Section 5.4. Remember that x[n] is the inverse Fourier transform of X(ej?) as defined in Eq. Note that because X(ej?) and X(ej?) are defined, the region of convergence of both X(z) and X(z) must include the unit circle.
(a) Argue that the singularities (poles) of X(z) will occur wherever X(z) has either poles or zeros. Use this fact to prove that if x[n] is causal, x[n] is minimum phase.
(b) Argue that if x[n] is minimum phase, the constraints of the region of convergence require x[n] to be causal.
We can examine this property for the case when x[n] can be written as a superposition of complex exponentials. Specifically, consider a sequence x[n] whose z-transform is?
Where A > 0 and ak,bk,ck and dk all have magnitude less than one .
(c) Write an expression for X(z) = log X(z).
(d) Solve for x[n] by taking the inverse z-tranform of your answer in part (c).
(e) Based on part (d) and the expression for X(z), argue that for sequences x[n] of this form, a causal complex cepstrum is equivalent to having minimum phase.
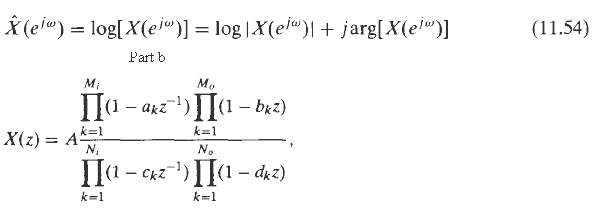
Step by Step Answer:

Discrete Time Signal Processing
ISBN: 978-0137549207
2nd Edition
Authors: Alan V. Oppenheim, Rolan W. Schafer





