Question: (a) Uniqueness, prove that the Laurent expansion of a given analytic function in a given annulus is unique.(b) Accumulation of singularities, does tan (1/z) have

(a) Uniqueness, prove that the Laurent expansion of a given analytic function in a given annulus is unique.(b) Accumulation of singularities, does tan (1/z) have a Laurent series that converges in a region 0 > |z| (c) Integrals expand the following function in a Laurent series that converges for |z| >0.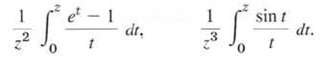 1 2 et - 1 t dr. 1 sin t t dt.

1 2 et - 1 t dr. 1 sin t t dt.

Step by Step Solution

★★★★★

3.43 Rating (175 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Team Project a fz z zogz gives fz nzzogz z zogz wh... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (1 attachment)

1-M-C-A-B-M (14).docx

120 KBs Word File

Students Have Also Explored These Related Complex Analysis Questions!

Prove that each of the following series converges and find its value, a) b) c) d) (-1)k-1 7 9k-1 COSR 5-3

In Problems 1-4, indicate whether the given series converges or diverges. If it converges, find its sum. Hint: It may help you to write out the first few terms of the series? 1. 2. 3. 4. k-2 23(- k=1

In Problems 1 - 4, show that each series converges absolutely? 1. 2. 3. 4. nVn n+ 2" n+1

\fCOMPLEX VARIABLES AND APPLICATIONS Eighth Edition James Ward Brown Professor of Mathematics The University of Michigan-Dearborn Ruel V. Churchill Late Professor of Mathematics The University of...

Prove by using the expansion method that , given that and Tu > 2,7(n)

11. Ben & Jerry's Morrie Baker, owner of the Canadian franchise rights for Ben & Jerry's, wants to add a lot of stores quickly. His product is Ben & Jerry's ice cream, a super-premium ice cream that...

4 . 2 4 Given F 1 = IIM ( 0 , 4 , 5 , 6 ) and F 2 = M ( 0 , 4 , 7 ) , find the maxterm expansion for F 1 + F 2 State a general rule for finding the maxterm expansion of F 1 + F 2 , given the max -...

= 2) We know that for an ideal gas Cp,m = Cv,m + R. The general relationship for any gas can be written, for 1 mole, as a (equation-1) Where Vm is the molar volume (the volume of 1 mole of the gas,...

Please kindly show all steps. 1 1.1 An asset annual's return, R, depends on two states of the economy. When the economy is in expansion, the return is exponentially distributed with mean 7%, and when...

How can an auditor obtain evidence about the operating effectiveness of controls at an outside service provider?

4. All dry martinis are dangerous concoctions. Th erefore, it is false that some dry martinis are not dangerous concoctions. Use the modern square of opposition to determine whether the following...

4.a. Find the unit tangent and normal vectors to r(t) = 4 cost i + sin t j at t = /2. Sketch a portion of the curve showing the point of tangency.

According to a survey, only 15% of customers who visited the website of a major retail store made a purchase. Random samples of size 50 are selected (show your workings clearly. a) What is the...

1 Use Taylor's formula for f(x,y) at the origin to find quadratic and cubic approximations of f(x.y) = near the origin. 1-3x-y

A glass vessel contains 16.0 g of CH 4 gas. Assuming ideal gas behavior, what would happen to the pressure exerted on the walls of the vessel if 2.0 g of hydrogen gas were added to the vessel? The...

According to Borjas (2003), immigration into the United States increased the labour supply of working men by 11.0% from 1980 to 2000 and reduced the wage of the average native worker by 3.2%. From...

The presence of taxes has what effect on the multiplier? They a. increase it. b. decrease it. c. destabilize it. d. negate it. e. have no effect on it.

Find the inverse transform, indicating the method used and showing the details: 3s s2 - 2s + 2

Using the Laplace transform and showing the details, find the current i(t) in the circuit in Fig. 126, assuming i(0) = 0 and: R = 1 kÎ© (= 1000 Î©), L = 1 H, v = 0 if 0

Given F(s) = L(f), find f(t). a, b, L, n are constants. Show the details of your work. 1 (s + V2(s V3)

(a) Give reasons why Theorems 1 and 2 are more important than Theorem 3. (b) Extend Theorem 1 by showing that if f(t) is continuous, except for an ordinary discontinuity (finite jump) at some t =...

Using the Laplace transform and showing the details, find the current i(t) in the circuit in Fig. 126, assuming i(0) = 0 and: R = 10 Î©, L = 0.5 H, v = 200t V if 0 2...

Intelekz Corporation plans to start a new project in Indonesia to enlarge its market share. The total cost of the new project is RM17 million. It is estimated that the after- tax cash inflows is...