A fluid at temperature T?? is flowing at a velocity U?? over a flat plate which is

Question:

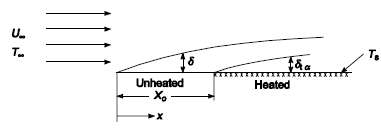
A fluid at temperature T?? is flowing at a velocity U?? over a flat plate which is at the same temperature as the fluid for a distance x0 from the leading edge, but at a higher temperature Ts beyond this point. Show by means of the integral boundary-layer equations that ζ, the ratio of the thermal boundary-layer thickness to the hydrodynamic boundary-layer thickness, over the heated portion of the plate is approximately

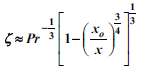
if the flow is laminar.GIVENLaminar flow over a flat plateFluid temperature = T??Fluid velocity = U??Plate temperature = T?? for x Plate temperature = Ts for x > XoASSUMPTIONSSteady stateThe temperature distribution is a third-order polynomial: T ?? Ts = αy + cy3Property value changes due to the temperature profile do not affect the hydrodynamic boundary layer.

Distribution
The word "distribution" has several meanings in the financial world, most of them pertaining to the payment of assets from a fund, account, or individual security to an investor or beneficiary. Retirement account distributions are among the most...