Let x [n] and h [n] be two real finite-length sequences such that x[n] = 0 for n outside the interval 0 ? n ? L ? 1, h[n] = 0 for n outside the interval 0 ? n ? p ? 1. We wish to compute the sequence y[n] = x[n] * h[n], where * denotes ordinary convolution.

(a) What is the length of the sequence y [n]?

(b) For direct evaluation of the convolution sum, how many real multiplications are required to compute all of the nonzero samples of y[n]? The following identity may be useful:

(c) State a procedure for using the DFT to compute all of the nonzero samples of y[n]. Determine the minimum size of the DFTs and inverse DFTs in terms of L and P.

(d) Assume that L = P = N/2, where N = 2^v is the size of the DFT. Determine a formula for the number of real multiplications required to compute all the nonzero values of y[n] using the method of part (c) if the DFTs are computed using a radix-2 FFT algorithm. Use this formula to determine the minimum value of N for which the FFT method requires fewer real multiplications than the direct evaluation of the convolution sum. ?

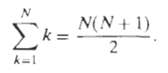
N(N + 1) k-1