Show that if and only if there is a sequence 0 < e n 0 such that
Question:
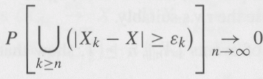
For the part en ![]() 0, show that, for every e > 0, there exists N = N(e) such that k ³ and n ³ imply
0, show that, for every e > 0, there exists N = N(e) such that k ³ and n ³ imply ![]() (|Xk €“ X| ³ e) Ã
(|Xk €“ X| ³ e) à ![]() (|Xk €“ X| ³ ek) and then use Theorem 4 suitably. For the part
(|Xk €“ X| ³ ek) and then use Theorem 4 suitably. For the part ![]() , use Theorem 4 in order to conclude that
, use Theorem 4 in order to conclude that
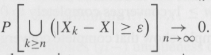
Applying this conclusion for m ³ 1, show that there exists a sequence nm †‘ ¥ as m †’ ¥ such that
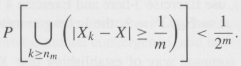
Finally, for nm £ k < nm +1, set ek = 1/m and show that

Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

An Introduction to Measure Theoretic Probability
ISBN: 978-0128000427
2nd edition
Authors: George G. Roussas
Question Posted:





