At time zero the price of a non-dividend-paying stock is S₀. Suppose that the time interval between 0 and T is divided into two subintervals of length t₁ and t₂. During the first subinterval, the risk-free interest rate and volatility are r₁ and σ₁, respectively. During the second subinterval, they are r₂ and σ₂, respectively. Assume that the world is risk neutral.

(a) Use the results in Chapter 15 to determine the stock price distribution at time T in terms of r₁, r₂, σ₁, σ₂, t₁, t₂, and S₀.

(b) Suppose that r̅ is the average interest rate between time zero and T and that V̅ is the average variance rate between times zero and T. What is the stock price distribution as a function of T in terms of r̅, V̅, T, and S₀? 

(c) What are the results corresponding to (a) and (b) when there are three subintervals with different interest rates and volatilities? 

(d) Show that if the risk-free rate, r, and the volatility, σ, are known functions of time, the stock price distribution at time T in a risk-neutral world is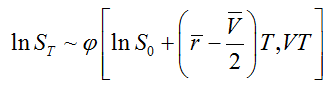 

where r̅ is the average value of r, V̅ is equal to the average value of σ², and S₀ is the stock price today.

Transcribed Image Text:

In S, - o| In S +| F - |T,VT