Refer to Probs. 18.141 and 18.142. (a) Show that the curve (called polhode) described by the tip of the vector with respect to a

Refer to Probs. 18.141 and 18.142.

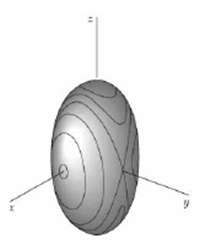
(a) Show that the curve (called polhode) described by the tip of the vector ω with respect to a frame of reference coinciding with the principal axes of inertia of the rigid body is defined by the equations and that the curve can, therefore, be obtained by intersecting the Poinsot ellipsoid with the ellipsoid defined by Eq. (2).

(b) Further show, assuming I_x > I_y > I_z, that the polhodes obtained for various values of O H have the shapes indicated in the figure.

(c) Using the result obtained in part b, show that a rigid body under no force can rotate about a fixed centroidal axis if, and only if, that axis coincides with one of the principal axes of inertia of the body, and that the motion will be stable if the axis of rotation coincides with the major or minor axis of the Poinsot ellipsoid (z or x axis in the figure) and unstable if it coincides with the intermediate axis (y axis).

"