Circulating axial flow in an annulus (Fig. 3B.6), a rod of radius KR moves upward with a constant velocity v₀ through a cylindrical container of inner radius R containing a Newtonian liquid, the liquid circulates in the cylinder, moving upward along the moving central rod and moving downward along the fixed container wall. Find the velocity distribution in the annular region, far from the end disturbances. Flows similar to this occur in the seals of some reciprocating machinery for example, in the annular space between piston rings. 

(a) First consider the problem where the annular region is quite narrow–that is, where K is just slightly less than unity. In that case the annulus may be approximated by a thin plane slit and the curvature can be neglected. Show that in this limit, the velocity distribution is given by where ζ = r/R. 

(b) Next work the problem without the thin-slit assumption. Show that the velocity distribution is given by   

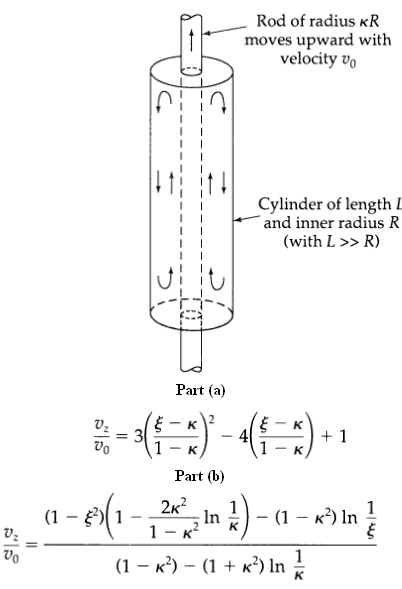
Rod of radius KR moves upward with velocity vo Cylinder of length I and inner radius R (with L>> R) Part (a) -() - + 1 3 Part (b) 2x? In 1 ? - (1 K) In (1 ) 1 Vz Vo (1 K?) (1 + K?) In