Consider a derivative that pays off Sⁿ_T at time T where S_T is the stock price at that time. When the stock pays no dividends and its price follows geometric Brownian motion, it can be shown that its price at time t (t ≤ T) has the form h(t, T) Sⁿ where S is the stock price at time  and  is a function only of t and T.

(a) By substituting into the Black–Scholes–Merton partial differential equation derive an ordinary differential equation satisfied by h(t, T). (b) What is the boundary condition for the differential equation for h(t, T)? (c) Show that

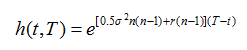
where r is the risk-free interest rate and σ is the stock price volatility.

h(t,T)= e0.5am{n-1)+r(n-1)|(7-{)