Consider an arbitrary digital filter with transfer function? (a) Perform a two-component polyphase decomposition of H(z) by
Question:
Consider an arbitrary digital filter with transfer function?
(a) Perform a two-component polyphase decomposition of H(z) by grouping the even-numbered samples h0(n) = h(2n) and the odd-numbered samples h1(n) = h(2n +1). Thus show that H(z) can be expressed as:
H(z) = H0(z2) + z?1H1(z2) and determine the H0(z) and H1(z).
(b) Generalized the result in part (a) by showing that H(z) can decomposed into an D-component polyphase filter structure with transfer function, Determine Hk(z).
(c) For the IIR filter with transfer function H(z) = 1/ 1?az?1
Determine H0(z) and H1(z) for the two-component decomposition.
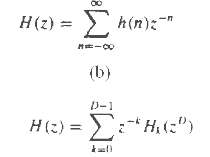
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Digital Signal Processing
ISBN: ?978-0133737622
3rd Edition
Authors: Jonh G. Proakis, Dimitris G.Manolakis
Question Posted:





