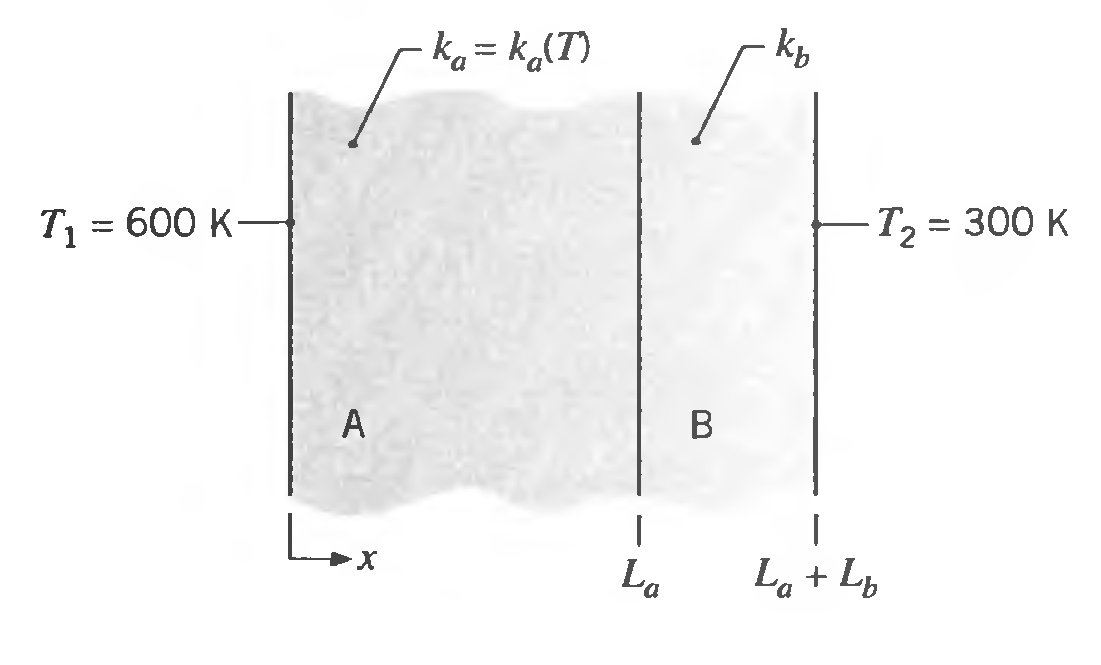
Consider one-dimensional conduction in a plane composite wall. The exposed surfaces of materials A and B are maintained at T₁ = 600 K and T₂ = 300 K respectively. Material A, of thickness L_a = 20 mm, has a temperature-dependent thermal conductivity of k_a = k_o [1 + a(T – T_o)], where ko = 4.4 W/m ∙ K, a = 0.008 K^-1 , T_o = 300 K and T is in Kelvin’s. Material B is of thickness L_b = 5 nun and has a thermal conductivity of kb = I W/m ∙ K.

(a) Calculate the heat flux through the composite wall by assuming material A to have a uniform thermal conductivity evaluated at the average temperature of the section.

(b) Using a space increment of 1 mm, obtain the finite-difference equations for the internal nodes and calculate the heat flux considering the temperature- dependent thermal conductivity for Material A. If the IHT software is employed, call-up functions from Tools/Finite-Difference Equations may be used to obtain the nodal equations. Compare your result with that obtained in part (a).

(c) As an alternative to the finite-difference method of part (b), use the finite-element method of FEHT to calculate the heat flux, and compare the result with that from part (a). Hint: In the Specify/Material

Properties box, properties may be entered as a function of temperature (T), the space coordinates (x, y), or time (t). See the He/p section for more details.

Transcribed Image Text:

kb ka = kq(T) T2 = 300 K T = 600 K- A B Lex La La + L,