Consider a potential well defined as U(x) = ? for x 0 for x > L (Fig.
Question:
Consider a potential well defined as U(x) = ? for x 0 for x > L (Fig. 40.27). Consider a particle with mass m and kinetic energy E
(a) The boundary condition at the infinite wall (x = 0) is ?(0) = 0. What must the form of the function ? (x) for 0
(b) The wave function must remain finite as x ? ?. What must the form of the function ? (x) for x > L be in order to satisfy both the Schrodinger equation and this boundary condition at infinity?(c) Impose the boundary conditions that ? and d?/dx are continuous at x = L. Show that the energies of the allowed levels are obtained from solutions of the equation k cot kL = - K. where k = ?2mE/h and K = ?2m (U0 ?? E)h.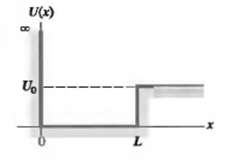
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





