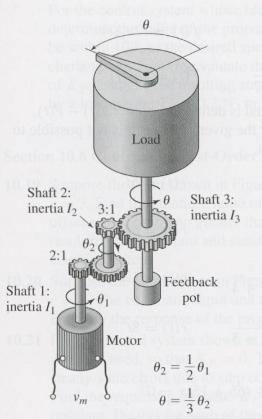
Figure shows a system for controlling the angular position of a load, such as an antenna. Figure

Question:

Figure shows a system for controlling the angular position of a load, such as an antenna. Figure shows the block diagram for PD control of this system using a field-controlled motor. Use the following values:

K_a = 1 V/V

R = 0.3 Ω

K_T = 0.6 N.m/A

K_pot = 2 V/rad

I₁ = 0.01 kg.m²

I₂ = 5 x l0^-4 kg.m²

l₃ = 0.2 kg.m²

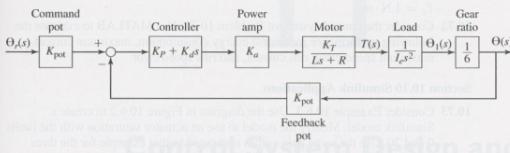
The inertia I_e in the block diagram is the equivalent inertia of the entire system, as felt on the motor shaft.

a. Assume that the motor inductance is very small and set L = 0. Compute I_e, obtain the transfer function Ɵ(s)/Ɵ_r(s), and compute the values of the control gains K_p and K_d to meet the following specifications: ζ = I and τ = 0.5 s.

b. Use the MATLAB t f function to create the model sys l from this transfer function.

c. Using the values of K_p and K_d computed in part (a), and the value L = 0.015 H, obtain the transfer function Ɵ(s)/Ɵ_r(s) and use the MATLAB t f function to create the model sys 2 from this transfer function.

d. Use the MATLAB step (sys l, sys2) function to plot the unit step response of both transfer functions. Right-click on the plots to obtain the maximum percent overshoot and settling time for each how close are the two responses? What is the effect of neglecting the inductance?

In Problem 7