Figure shows the magnitude |V[k]| of the 128-point DFT V[k] for a signal v[n]. The signal v[n] was obtained by multiplying x[n] by a 128-point rectangular window w[n]; i.e., v[n] = x[n]w[n]. Note that Figure shows |V[k]| only for the interval 0 ? k ? 64. Which of the following signals could be x[n]? That is, which are consistent with the information shown in the figure?Figure shows the magnitude |V[k]| of the 128-point DFT V[k] for a signal v[n]. The signal v[n] was obtained by multiplying x[n] by a 128-point rectangular window w[n]; i.e., v[n] = x[n]w[n]. Note that Figure shows |V[k]| only for the interval 0 ? k ? 64. Which of the following signals could be x[n]? That is, which are consistent with the information shown in the figure?

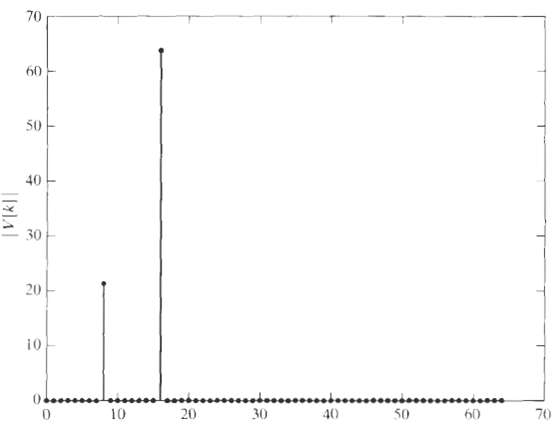
x₁[n] = cos (? n/4) + cos(0.26? n),

x₂[n] = cos (? n/4) + (1/3) sin(? n/8),

x₃[n] = cos (? n/4) + (1/3) cos(? n/8),

x₄[n] = cos(? n/8) + (1/3) cos(? n16),

x₅[n] = (1/3) cos (? n/4) + cos(? n/8),

x₆[n] = cos (? n/4) + (1/3) cos(? n/8 + ?/3),

Transcribed Image Text:

70 60 50 40 30 20 10 10 20 30 40 50 70 60 |V[k]|