I express my undying love for my wife through weekly purchases of roses that cost $5 each.

Question:

A. Suppose you have known me for a long time and you have seen my economic circumstances change with time. For instance, you knew me in graduate school when I managed to have $125 per week in disposable income that I could choose to allocate between purchases of roses and “other consumption” denominated in dollars. Every week I brought 25 roses home to my wife.

(a) Illustrate my budget as a graduate student — with roses on the horizontal and “dollars of other consumption” on the vertical axis. Indicate my optimal bundle on that budget as A. Can you conclude whether either good is not “essential”?

(b)When I became an assistant professor, my disposable income rose to $500 per week, and the roses I bought for my wife continued to sell for $5 each. You observed that I still bought 25 roses each week. Illustrate my new budget constraint and optimal bundle B on your graph. From this information, can you conclude whether my tastes might be quasilinear in roses? Might they not be quasilinear?

(c) Suppose for the rest of the problem that my tastes in fact are quasilinear in roses. One day while I was an assistant professor, the price of roses suddenly dropped to $2.50. Can you predict whether I then purchased more or fewer roses?

(d) Suppose I had not gotten tenure—and the best I could do was rely on a weekly allowance of $50 from my wife. Suppose further that the price of roses goes back up to $5. How many roses will I buy for my wife per week?

(e) True or False: Consumption of quasilinear goods always stays the same as income changes.

(f) True or False: Over the range of prices and incomes where corner solutions are not involved, a decrease in price will result in increased consumption of quasilinear goods but an increase in income will not.

B. Suppose my tastes for roses (x₁) and other goods (x₂) can be represented by utility function u(x₁,x₂) = βx^α₁ +x₂.

(a) Letting the price of roses be denoted by p₁, the price of other goods by 1, and my weekly income by I , determine my optimal weekly consumption of roses and other goods as a function of p₁ and I .

(b) Suppose β = 50 and α = 0.5. How many roses do I purchase when I = 125 and p₁ = 5? What if my income rises to $500?

(c) Comparing your answers to your graph from part A, could the actions observed in part A (b) be rationalized by tastes represented by the utility function u(x₁,x₂)? Give an example of another utility function that can rationalize the behavior described in part A(b).

(d) What happens when the price of roses falls to $2.50? Is this consistent with your answer to part A(c)?

(e) What happens when my income falls to $50 and the price of roses increases back to $5? Is this consistent with your answer to part A(d)? Can you illustrate in a graph how the math is giving an answer that is incorrect?

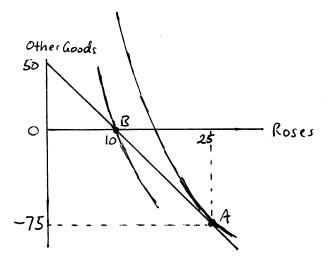
Other Goods 50 Roses -75-