In Section 5.1, we studied linear combinations of independent random variables. What happens if the variables are not independent? A lot of mathematics can be used to prove the following:

Let x and y be random variables with means mx and my, variances σ_x² and σ_y² and population correlation coefficient r (the Greek letter rho). Let a and b be any constants and let w = ax + by. Then,

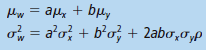
In this formula, r is the population correlation coefficient, theoretically computed using the population of all (x, y) data pairs. The expression σ_xσ_y ρ  is called the covariance of x and y. If x and y are independent, then ρ = 0 and the formula for σ_w² reduces to the appropriate formula for independent variables (see Section 5.1). In most real-world applications, the population parameters are not known, so we use sample estimates with the understanding

that our conclusions are also estimates.

Do you have to be rich to invest in bonds and real estate? No, mutual fund shares are available to you even if you aren’t rich. Let x represent annual percentage return (after expenses) on the Vanguard Total Bond Index Fund, and let y represent annual percentage return on the fidelity Real estate Investment Fund. Over a long period of time, we have the following population estimates (based on Morningstar Mutual Fund Report).

μ_x = 7.32 σ_x » 6.59 μ_y » 13.19 μ_y » 18.56 ρ » 0.424

(a) Do you think the variables x and y are independent? Explain.

(b) Suppose you decide to put 60% of your investment in bonds and 40% in real estate. This means you will use a weighted average w = 0.6x + 0.4y.

Estimate your expected percentage return μ_w and risk σ_w.

(c) Repeat part (b) if w = 0.4x + 0.6y.

(d) Compare your results in parts (b) and (c). Which investment has the higher expected return? Which has the greater risk as measured by σ_w?

Transcribed Image Text:

Hw = al, + buly o, = a'o, + b’o, + 2abo,0,p %3D