In the discussion of free electrons in Section 42.5, we assumed that we could ignore the effects
Question:
In the discussion of free electrons in Section 42.5, we assumed that we could ignore the effects of relativity. This is not a safe assumption if the Fermi energy is greater than about 1/100 mc2 (that is, more than about 1% of the rest energy of an electron).(a) Assume that the Fermi energy at absolute zero, as given by Eq. (42.20), is equal to 1/100 mc2 ?? Show that the electron concentration is and determine the numerical value of N/V.(b) Is it a good approximation to ignore relativistic effects for electrons in a metal such as copper, for which the electron concentration is 8.45 x 1028 m-3? Explain.(c) A white dwarf star is what is left behind by a star like the sun after it has ceased to produce energy by nuclear reactions. (Our own sun will become a white dwarf star in another 6 x 109 years or so.) A typical white dwarf has mass 2 x 1030 kg (comparable to the sun) and radius 6000 km (comparable to that of the earth). The gravitational attraction of different parts of the white dwarf for each other tends to compress the star; what prevents it from compressing is the pressure of free electrons within the star (see Problem 42.53). Estimate the electron concentration within a typical white dwarf star using the following assumptions: (i) the white dwarf star is made of carbon, which has a mass per atom of 1.99 x 10-26 kg; and (ii) all six of the electrons from each carbon atom are able to move freely throughout the star.(d) Is it a good approximation to ignore relativistic effects in the structure of a white dwarf star?Explain.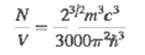
Step by Step Answer:

Probability And Statistics
ISBN: 9780321500465
4th Edition
Authors: Morris H. DeGroot, Mark J. Schervish





