In this exercise, we are working with the concept of an elasticity of substitution. This concept was introduced in part B of the Chapter. Thus, this entire question relates to material from part B, but the A-part of the question can be done simply by knowing the formula for an elasticity of substitution while the B-part of the question requires further material from part B of the Chapter. In Section 5B.1, we defined the elasticity of substitution as

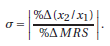
A: Suppose you consume only apples and oranges. Last month, you consumed bundle A=(100,25) €” 100 apples and 25 oranges, and you were willing to trade at most 4 apples for every orange. Two months ago, oranges were in season and you consumed B=(25,100) and were willing to trade at most 4 oranges for 1 apple. Suppose your happiness was unchanged over the past two months.

(a) On a graph with apples on the horizontal axis and oranges on the vertical, illustrate the in- difference curve on which you have been operating these past two months and label the MRS where you know it.

(b) Using the formula for elasticity of substitution, estimate your elasticity of substitution of apples for oranges.

(c) Suppose we know that the elasticity of substitution is in fact the same at every bundle for you and is equal to what you calculated in (b). Suppose the bundle C=(50,50) is another bundle that makes you just as happy as bundles A and B. What is the MRS at bundle C?

(d) Consider a bundle D = (25,25). If your tastes are homothetic, what is the MRS at bundle D?

(e) Suppose you are consuming 50 apples, you are willing to trade 4 apples for one orange and you are just as happy as you were when you consumed at bundle D. How many oranges are you consuming (assuming the same elasticity of substitution)?

(f) Call the bundle you derived in part (e) E. If the elasticity is as it was before, at what bundle would you be just as happy as at E but would be willing to trade 4 oranges for 1 apple?

B: Suppose your tastes can be summarized by the utility function

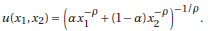
(a) In order for these tastes to contain an indifference curve such as the one containing bundle A that you graphed in A(a), what must be the value of ρ? What about α?

(b) Suppose you were told that the same tastes can be represented by u(x₁, x₂) = x^γ₁x^δ₂. In light of your answer above, is this possible? If so, what has to be true about γ and δ given the symmetry of the indifference curves on the two sides of the 45 degree line?

(c) What exact value(s) do the exponents γ and δ take if the label on the indifference curve containing bundle A is 50? What if that label is 2,500? What if the label is 6,250,000?

(d) Verify that bundles A, B and C (as defined in part A) indeed lie on the same indifference curve when tastes are represented by the three different utility functions you implicitly derived in B(c). Which of these utility functions is homogeneous of degree 1? Which is homogeneous of degree 2? Is the third utility function also homogeneous?

(e) What values do each of these utility functions assign to the indifference curve that contains bundle D?

(f) True or False: Homogeneity of degree 1 implies that a doubling of goods in a consumption basket leads to €œtwice€ the utility as measured by the homogeneous function, whereas homogeneity greater than 1 implies that a doubling of goods in a consumption bundle leads to more than €œtwice€ the utility.

(g) Demonstrate that the MRS is unchanged regardless of which of the three utility functions derived in B(c) is used.

(h) Can you think of representing these tastes with a utiliy function that assigns the value of 100 to the indifference curve containing bundle A and 75 to the indifference curve containing bundle D? Is the utility function you derived homogeneous?

(i) True or False: Homothetic tastes can always be represented by functions that are homogeneous of degree k (where k is greater than zero), but even functions that are not homogeneous can represent tastes that are homothetic.

(j) True or False: The marginal rate of substitution is homogeneous of degree 0 if and only if the underlying tastes are homothetic.

Transcribed Image Text:

5%Δ (τ/x)| σ- %ΔMRS