In this exercise we work with the Black-Scholes setting applied to foreign currency denominated assets. We will
Question:
In this exercise we work with the Black-Scholes setting applied to foreign currency denominated assets. We will see a different use of Girsanov theorem. [for more detail see Musiela and Rutkowski (1997).] Let r,f denote the domestic and the foreign risk-free rates. Let St be the exchange rate, that is, the price of 1 unit of foreign currency in terms of domestic currency. Assume a geometric process for the dynamics of St;
dSt = (r ? f)Stdt + ?StdWt.
(a) Show that where Wt is Wiener process under probability P.
(b) Is the process a martingale under measure P?
(c) Let P be the probability what does Girsonov theorem imply about the process, Wt ? ?t,
?under P?
?(d) shown using Ito formula that
dZt = Zt[(f ? r + ?2)dt ? ?dWt]
where Zt = 1/St.
(e) Under which probability is the process Ztert f eft a martingale?
(f) Can we say that P is the arbitrage-free measure of the foreign economy?
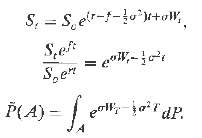
Step by Step Answer:

An Introduction to the Mathematics of financial Derivatives
ISBN: 978-0123846822
2nd Edition
Authors: Salih N. Neftci





