Interrelation of slit and annulus formulas, when an annulus is very thin, it may, to a good approximation, is considered as a thin slit. Then the results of Problem 2B.3 can be taken over with suitable modifications. For example, the mass rate of flow in an annulus with outer wall of radius R and inner wall of radius (1 - ?) R, where ? is small, may be obtained from Problem 2B.3 by replacing 2B by ?R, and W by 2? (1 ? ? ?) R. In this way we get for the mass rate of flow: Show that this same result may be obtained from Eq. 2.4-17 by setting K equal to 1 ? ? everywhere in the formula and then expanding the expression for w in powers of ?. This requires using the Taylor series (see SC.2) and then performing a long division. The first term in the resulting series will be Eq. 2B.5-1. Caution: In the derivation it is necessary to use the first four terms of the Taylor series in Eq. 2B.5-2. ?

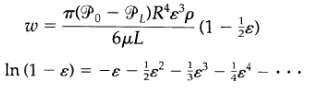
W= T(P-P)Rp 6L (1 - ) In (18)= -88--- 1.3