Question: Let the real discrete-time signal x[n] with Fourier transform X(e j? ) be the input to a system with the output defined by (a) Sketch

Let the real discrete-time signal x[n] with Fourier transform X(e^j?) be the input to a system with the output defined by

x[n]. if n is even, 0, y[n] = otherwise.

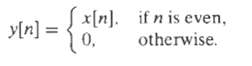
(a) Sketch the discrete-time signal s[n] = 1 + cos(? n) and its (generalized) Fourier transform S(e ^j?),

(b) Express Y(e^j?), the Fourier transform of the output, as a function of X(e^j?) and S(e^j?).

(c) You would like to approximate x[n] by the interpolated signal w[n] = y[n] + (1/2)(y[n + 1] + y[n ? 1]). Determine the Fourier transform W(e^j?) as a function of Y(e^j?).

(d) Sketch X(e^j?), y(e^j?), and W(e^j?) for the case when x[n] = sin(?n/a)/(?n/a) and a > 1. under what conditions is the proposed interpolated signal w[n] a good approximation for the original x[n]

x[n]. if n is even, 0, y[n] = otherwise.

Step by Step Solution

★★★★★

3.34 Rating (163 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a Notice that b Since yn ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (1 attachment)

30-E-T-E-D-S-P (47).docx

120 KBs Word File

Students Have Also Explored These Related Telecommunication Engineering Questions!

To accurately approximate sin x and cos x for inclusion in a mathematical library, we first restrict their domains. Given a real number x, divide by to obtain the relation |x| = M + s, where M is an...

Determine the signal f(t) whose Fourier transform is shown in Fig. 18.38. (Hint: Use the duality property.) F(a) 10 F 2 1 02

A signal f(t) has Fourier transform F() = 1 / 2+ j Determine the Fourier transform of the following signals: (a) x(t) = f(3t - 1) (b) y(t) = f(t) cos 5t (c) z(t) = d / dt f(t) (d) h(t) = f(t) * f(t)...

Let i and j be positive integers. (i) Prove that there exist natural numbers a and b such that ai = bj+gcd(i, j). You may use standard results provided that you state them clearly. [4 marks] (ii) Let...

Briefly describe ASCII and Unicode and draw attention to any relationship between them. [3 marks] (b) Briefly explain what a Reader is in the context of reading characters from data. [3 marks] A...

A discrete sequence {xn} can be converted into a continuous representation x(t) = ts X n= (t n ts) xn, where ts is the sampling period. (a) State two characteristic properties of Dirac's function. [2...

can someone solve this Modern workstations typically have memory systems that incorporate two or three levels of caching. Explain why they are designed like this. [4 marks] In order to investigate...

Pogram P3.1 can he used to evaluale and plot the DTFT of the farm of E4 33 % Progr P3.1 Evaluation of the % compute the trequescy samples of the TFT aubplot (2,1 0 Chapter 3Discrete-Time Signals in...

QUIZ... Let D be a poset and let f : D D be a monotone function. (i) Give the definition of the least pre-fixed point, fix (f), of f. Show that fix (f) is a fixed point of f. [5 marks] (ii) Show that...

(a) In SystemVerilog, what is the difference between: (i) The ternary operator ? and if...then...else statements? [2 marks] (ii) always_ff and always_comb? [2 marks] (iii) Blocking, non-blocking and...

If the price of corn rose, a. What would be the effect on the supply of corn? b. What would be the effect on the supply of wheat?

Create a "Forms of Business Organziation Chart" prepare a chart comparing the Major Forms of Business. include: 1) sole proprietorships; 2) partnerships; 3) limited partnerships; 4) limited liability...

A position control system can be analyzed using the feedback system in Figure 10.38, where the process transfer function is 5 G(s): = s(s + 1)(0.4s + 1)* A phase-lag compensator that provides a phase...

Calculating Payback An investment project provides cash inflows of $860 per year for eight years. What is the project payback period if the initial cost is $3,000? What if the initial cost is $5,000?...

For the MgOAl2O3 system, what is the maximum temperature that is possible without the formation of a liquid phase? At what composition or over what range of compositions will this maximum temperature...

In a set of data analyzed by the Statistics Consulting Center at Virginia Polytechnic Institute and State University (VPI&SU), a group of subjects was asked to complete a certain task on the...

It is claimed that a new diet will reduce a person's weight by 4.5 kilograms on the average in a period of 2 weeks. The weights of 7 women who followed this diet were recorded before and after a...

Past data indicate that, the amount of money contributed by the working residents of a large city to a volunteer rescue squad is a normal random variable with a standard deviation of S1.40. It has...

33. Which of the following might worsen a nations trade deficit? A. Lower wages relative to other nations. B. Lower taxes on corporate profits relative to other nations. C. A higher interest rate on...

Consider the signal with Fourier transform X () = X R () + j( X 1 ()). Determine and sketch the signal y(n) with Fourier transform Y () = X 1 () + X 1 () e j2 x(n) = {1,0. 1, 2, 3}

Determine the signal x(n) if its Fourier transform is as given in figure. Xiw) 8 8 10 10 10 (a) X,w) (b) X(w) - 2 - -w. (c)

Consider the signal with Fourier transform X(?). Compute the following quantities, without explicitly computing X(?): x(n) = (-1, 2, -3, 2, -1} (m) X7 (q) (c) " X () dw (d) X(7) (a) X (0) |(e) X() dw

A firm has determined its cost of each source of capital and optimal capital structure which is composed of the following sources and target market value proportions: Source of Capital Target Market...

Holding Period Return Suppose that on January 1, 2019, you purchased 6.375 coupon Government of Canada bond with semi-annual payments, and a maturity date of December 31, 2026. At that time, the YTM...

2 Incorrect Question 1 0/1 pts If a bank has $200,000 of checkable deposits, it wants to maintain at least 20 percent of checkable deposits as reserves, and it holds $80,000 in reserves, then the...