Professor Gill has taught general psychology for many years. During the semester, she gives three multiple-choice exams, each worth 100 points. At the end of the course, Dr. Gill gives a comprehensive fi­nal worth 200 points. Let x₁, x₂, and x₃ represent a student’s scores on exams 1, 2, and 3, respectively. Let x4 represent the student’s score on the ­final exam. Last semester Dr. Gill had 25 students in her class. The student exam scores are shown on the next page.

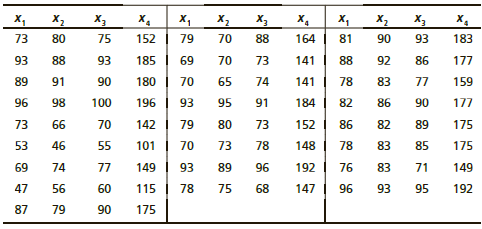
(a) Generate summary statistics, including the mean and standard deviation of each variable. Compute the coefficient of variation (see Section 3.2) for each variable. Relative to its mean, which variable has the greatest spread of data values? Which variable has the smallest spread of data values relative to its mean?

(b) For each pair of variables, generate the sample correlation coefficient r. Compute the corresponding coefficient of determination r₂, Which variable (other than x,) has the greatest influence (by itself) on x₁? Would you say that both variables x₂ and x₃ show a strong influence on x,? Explain your answer. What percent of the variation in x₁ can be explained by the corresponding variation in x₂? Answer the same question for x₃.

(c) Perform a regression analysis with x, as the response variable. Use x₂ and as explanatory variables. Look at the coefficient of multiple determination. What percentage of the variation in x can be explained by the corresponding variations in 12 and x₃ taken together?

(d) Look at the coefficients of the regression equation. Write out the regress ion equation. Explain how each coefficient can be thought of as a slope. If age was held fixed, but a person put on 10 pounds, what would you expect for the corresponding change in systolic blood pressure? If a person kept the same weight but got 10 years older, what would you expect for the corresponding change in systolic blood pressure?

(e) Test each coeffi­cient in the regression equation to determine if it is zero or not zero. Use level of signifi­cance 5%. Why would the outcome of each hypothesis test help us decide whether or not a given variable should be used in the regression equation?

(f) Find a 90% con­fidence interval for each coef­ficient.

(g) This semester Susan has scores of 68, 72, and 75 on exams 1, 2, and 3, respectively. Make a prediction for Susan’s score on the ­final exam and fi­nd a 90% confi­dence interval for your prediction (if your software supports prediction intervals).

Transcribed Image Text:

X. 75 152 79 70 88 164 81 90 93183 93 185 I 69 7073 1488 92 86 177 90 180 70 65 74 14 78 83 77 159 96 98 100 19693 95 91 184| 82 86 90 177 73 66 70 142 79 80 73 15286 82 89175 55 101 70 73 78 148 78 83 85 175 77 149| 93 89 96 192 76 83 71 149 47 56 60 115 78 75 68 147 96 93 95192 73 80 93911002 89 91 53 46 69 74 87 79 90 175