Quitting Time: When to Exit a Declining Industry¹We illustrated in the text the strategic issues that arise for a monopolist who is threatened by a potential entrant into the market€”and in Chapter 26, we will investigate firm entry into an industry where demand increases. In this exercise, suppose instead that an industry is in decline in the sense that demand for its output is decreasing over time. Suppose there are only two firms left€”a large firm L and a small firm S.

A: Since our focus is on the decision of whether or not to exit, we will assume that each firm has fixed capacity kⁱ at which it produces output in any period in which it is still in business; i.e. if a firm i produces, it produces x = kⁱ . Since L is larger than S, we assume k^L > k^S. The output that is produced is produced at constant marginal cost MC = c. (Assume throughout that, once a firm has exited the industry, it can never produce in this industry again.)

(a) Since demand is falling over time, the price that can be charged when the two firms together produce some output quantity x declines with time €” i.e. p₁(x) > p₂(x) > p₃(x) > ... where subscripts indicate the time periods t = 1, 2, 3, If firm is the only firm remaining in period t , what is its profit Ï€i_t ? What if both firms are still producing in period t?

(b) Let tⁱ denote the last period in which demand is sufficiently high for firm i to be profitable (i.e. to make profit greater than or equal to zero) if it were the only firm in the market. Assuming they are in fact different, which is greater: t^L or t S?

(c) What are the two firms€™ sub game perfect strategies beginning in period (t S +1)?

(d) What are the two firms€™ sub game perfect strategies in periods (t^L +1) to t S?

(e) Suppose both firms are still in business at the beginning of period t^L before firms make their decision of whether to exit. Could both of them producing in this period be part of a sub game perfect equilibrium? If not, which of the two firms must exit?

(f) Suppose both firms are still in business at the beginning of period (t^Lˆ’1) (before exit decisions are made). Under what condition will both firms stay? What has to be true for one of them to exit€”and if one of them exits, which one?

(g) Let t denote the last period in which (p_t (k^S +k^L) ˆ’c) ‰¥ 0. Describe what happens in a sub game perfect equilibrium, beginning in period t = 1, as time goes by €” i.e. as t, t^L and t^S pass. Is there ever a time when price rises as the industry declines?

(h) Suppose that the small firm has no access to credit markets€”and therefore is unable to take on any debt. If the large firm knows this, how will this change the sub game perfect equilibrium? True or False: Although the small firm will not need to access credit markets in order to be the last firm in the industry, it will be forced out of the market before the large firm exits if it does not have access to credit markets.

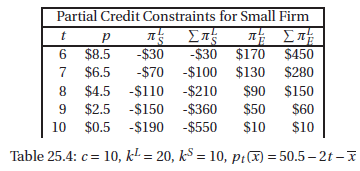
B: Suppose c = 10, k^L = 20, k= = 10 and p_t (x) = 50.5ˆ’2t ˆ’x until price is zero.

(a) How does this example represent a declining industry?

(b) Calculate t^S, t^L and t as defined in part A of the exercise.

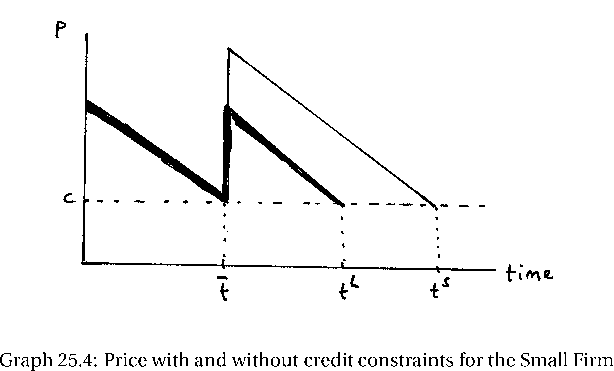
(c) Derive the evolution of output price as the industry declines.

(d) How does your answer change when firm S has the credit constraint described in A (h) €” i.e. when the small firm has no access to credit markets.

(e) How would your answer change if the large rather than the small firm had this credit constraint?

(f) Suppose firm S can only go into debt for n time periods. Let n be the smallest n for which the sub game perfect equilibrium without credit constraints holds, with n < n implying the change in equilibrium you described in part A (h). What is n? (Assume no discounting).

(g) If n < n, how will output price evolve as the industry declines?

Transcribed Image Text:

time Graph 25.4: Price with and without credit constraints for the Small Firm