Relativity and the Wave Equation(a) Consider the Galilean transformation along the x-direction: x' = x ?? vt and t' = t. In frame S the wave equation for electromagnetic waves in a vacuum is where E represents the electric field in the wave. Show that by using the Galilean transformation the wave equation in frame S' is found to be this has a different form than the wave equation in S. Hence the Galilean transformation violates the first relativity postulate that all physical laws have the same form in all inertial reference frames.(b) Repeat the analysis of part (a), but use the Lorentz coordinates transformations, Eqs. (37.21), and show that in frame S' the wave equation has the same form as in frame S: Explain why this shows that the speed of light in vacuum is e in both frames S andS'.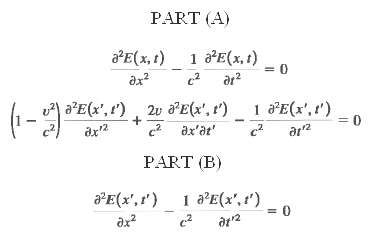

PART (A) aE(x, t) x 1 aE(x, t) C dr 1 _v) aE(x, 1) aE(x', t') 2v aE(x', t') + dx2 c ax'at' PART (B) aE(x',') 1 aE(x', 1) x C at2 0 1 aE(x', t') C 31 = 0 0