Rotating cone pump (see Fig. 2C.6), find the mass rate of flow through this pump as a function of the gravitational acceleration, the impressed pressure difference, the angular velocity of the cone, the fluid viscosity and density, the cone angle, and other geometrical quantities labeled in the figure. 

(a) Begin by analyzing the system without the rotation of the cone. Assume that it is possible to apply the results of Problem 2B.3 locally. That is, adapt the solution for the mass flow rate from that problem by making the following replacements: 

Replace (P₀ – P_L) L by – dP/dz 

Replace W by  2πr = 2πz sin β thereby obtaining 

The mass flow rate w is a constant over the range of z. Hence this equation can be integrated to give 

(b) Next, modify the above result to account for the fact that the cone is rotating with angular velocity Ω. The mean centrifugal force per unit volume acting on the fluid in the slit will have a z-component approximately given by what is the value of K? Incorporate this as an additional force tending to drive the fluid through the channel. Show that this leads to the following expression for the mass rate of flow:   

Here P₁, = p₁ + pgL₁, cos β.

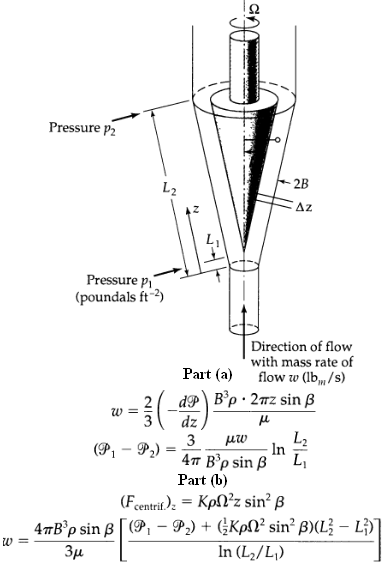
Pressure p2 2B L2 Az Pressure p (poundals ft-2) Direction of flow with mass rate of Part (a) flow w (lb, /s) d?) ' 2z sin B dz L2 In L, 4 'p sin B 3 (P1 P2) = Part (b) (Feentrit); = KpNz sin? 47Bp sin [ (P1 P2) + GKpN sin? B)(L} L})] In (L2/L,)