Shape of free surface in tangential annular flow (a) A liquid is in the annular space between
Question:
Shape of free surface in tangential annular flow
(a) A liquid is in the annular space between two vertical cylinders of radii KR and R, and the liquid is open to the atmosphere at the top. Show that when the inner cylinder rotates with an angular velocity Ω, and the outer cylinder is fixed, the free liquid surface has the shape in which zR is the height of the liquid at the outer-cylinder wall, and ζ = r/R.
(b) Repeat (a) but with the inner cylinder fixed and the outer cylinder rotating with an angular velocity Ωo. Show that the shape of the liquid surface is
Draw a sketch comparing these two liquid-surface shapes.
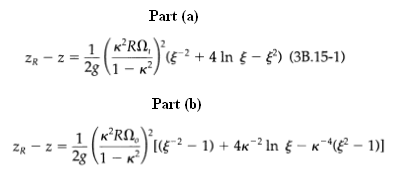
Transcribed Image Text:
Part (a) 1 (K*RN, ZR - z 2g " |(5²+ 4 In § – ³) (3B.15-1) Part (b) 1(K°RN,' 2g \1 - K (2 – 1) + 4K-2 In § - K*( – 1)]
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Answer rating: 100% (13 reviews)
Shape of free surface in tangential annular flow a The velocity distribution is given by Eq 3632 and ...View the full answer

Answered By

Ashington Waweru
I am a lecturer, research writer and also a qualified financial analyst and accountant. I am qualified and articulate in many disciplines including English, Accounting, Finance, Quantitative spreadsheet analysis, Economics, and Statistics. I am an expert with sixteen years of experience in online industry-related work. I have a master's in business administration and a bachelor’s degree in education, accounting, and economics options.
I am a writer and proofreading expert with sixteen years of experience in online writing, proofreading, and text editing. I have vast knowledge and experience in writing techniques and styles such as APA, ASA, MLA, Chicago, Turabian, IEEE, and many others.
I am also an online blogger and research writer with sixteen years of writing and proofreading articles and reports. I have written many scripts and articles for blogs, and I also specialize in search engine
I have sixteen years of experience in Excel data entry, Excel data analysis, R-studio quantitative analysis, SPSS quantitative analysis, research writing, and proofreading articles and reports. I will deliver the highest quality online and offline Excel, R, SPSS, and other spreadsheet solutions within your operational deadlines. I have also compiled many original Excel quantitative and text spreadsheets which solve client’s problems in my research writing career.
I have extensive enterprise resource planning accounting, financial modeling, financial reporting, and company analysis: customer relationship management, enterprise resource planning, financial accounting projects, and corporate finance.
I am articulate in psychology, engineering, nursing, counseling, project management, accounting, finance, quantitative spreadsheet analysis, statistical and economic analysis, among many other industry fields and academic disciplines. I work to solve problems and provide accurate and credible solutions and research reports in all industries in the global economy.
I have taught and conducted masters and Ph.D. thesis research for specialists in Quantitative finance, Financial Accounting, Actuarial science, Macroeconomics, Microeconomics, Risk Management, Managerial Economics, Engineering Economics, Financial economics, Taxation and many other disciplines including water engineering, psychology, e-commerce, mechanical engineering, leadership and many others.
I have developed many courses on online websites like Teachable and Thinkific. I also developed an accounting reporting automation software project for Utafiti sacco located at ILRI Uthiru Kenya when I was working there in year 2001.
I am a mature, self-motivated worker who delivers high-quality, on-time reports which solve client’s problems accurately.
I have written many academic and professional industry research papers and tutored many clients from college to university undergraduate, master's and Ph.D. students, and corporate professionals. I anticipate your hiring me.
I know I will deliver the highest quality work you will find anywhere to award me your project work. Please note that I am looking for a long-term work relationship with you. I look forward to you delivering the best service to you.
3.00+
2+ Reviews
10+ Question Solved
Related Book For 

Question Posted:
Students also viewed these Chemical Engineering questions
-
The outer gear C rotates with an angular velocity of 5 rad/s clockwise. Knowing that the inner gear A is stationary, determine (a) The angular velocity of the intermediate gear B, (b) The angular...
-
The arm ABC rotates with an angular velocity of 4 rad/s counterclockwise. Knowing that the angular velocity of the intermediate gear B is 8 rad/s counterclockwise, determine(a) The instantaneous...
-
The intermediate gear B rotates with an angular velocity of 20 rad/s clockwise. Knowing that the outer gear C is stationary, determine (a) The angular velocity of the inner gear A, (b) The angular...
-
TCP: the client sends only 1 message to the server hello from TCP Client and the server responds with the uppercase message. Update the program / make a simple chat program so that The client can...
-
In many countries higher education is heavily subsidized by the government (that is, university students do not bear the full cost of their college education). While there may be good reasons for...
-
Use the index of any tax service to locate authorities dealing with the deductibility of the cost of a facelift. a. Cite the authority you find. b. List the primary IRC section cited as authority. c....
-
What is the difference between a stock dividend and a stock split? As a stockholder, would you prefer to see your company declare a 100% stock dividend or a two-for-one split? Assume that either...
-
Merline, a one-product mail-order firm, buys its product for $ 75 per unit and sells it for $ 150 per unit. The sales staff receives a 10% commission on the sale of each unit. Its December income...
-
24. Fulkerson Metals maintains accurate records of the inventory maintains accurate records of the inventory purchased from its suppliers and sold to customers. The records show the following...
-
Suppose that Aviva can earn supplemental in-come by working overtime. She intends to use any income she earns to buy shares of stock in a corporation, with the intention of leaving the shares to her...
-
Torricelli's equation for efflux from a tank (Fig. 3B.14) a large uncovered tank is filled with a liquid to a height h. Near the bottom of the tank, there is a hole that allows the fluid to exit to...
-
Flow in a slit with uniform cross flow (Fig. 3B.16). A fluid flows in the positive x-direction through a long flat duct of length L, width W, and thickness B, where L > > W >> B. The duct has porous...
-
In what ways do employment laws differ in a global environment?
-
The following information appears in the records of Poco Corporation at year-end: a. Calculate the amount of retained earnings at year-end. b. If the amount of the retained earnings at the beginning...
-
For the following four unrelated situations, A through D, calculate the unknown amounts appearing in each column: A B D Beginning Assets... $38,000 $22,000 $38,000 ? Liabilities.. 22,000 15,000...
-
On December 31, John Bush completed his first year as a financial planner. The following data are available from his accounting records: a. Compute John's net income for the year just ended using the...
-
Statement of Stockholders' Equity and Balance Sheet The following is balance sheet information for Flush Janitorial Service, Inc., at the end of 2019 and 2018: Required a. Prepare a balance sheet as...
-
Petty Corporation started business on January 1, 2019. The following information was compiled by Petty's accountant on December 31, 2019: Required a. You have been asked to assist the accountant for...
-
What is amutually exclusive project?Howshouldmanagers rankmutually exclusive projects? AppendixlLO1
-
Discrete sample spaces: suppose there are N cable cars in San Francisco, numbered sequentially from 1 to N. You see a cable car at random; it is numbered 203. You wish to estimate N. (See Goodman,...
-
What is the density of oxygen gas (O 2 ) at 298 K and 0.987 bar?
-
It is often said that inflation greases the wheels of the labor market. Explain what this statement means.
-
Suppose that the inflation rate in an economy has been 4% for several years. The central bank unexpectedly increases the rate of growth of the money supply by 2%. Describe the effect on each of the...
-
The idea of shoe-leather costs is that people wear out their shoes going back and forth to the bank. While this is unlikely in reality, what are some examples of actual costs that you might incur by...
-
Practice Problem 1 The stockholders equity accounts of Bramble Corp. on January 1, 2017, were as follows. Preferred Stock (6%, $100 par noncumulative, 4,400 shares authorized) $264,000 Common Stock...
-
JVCU Which of the following is considered cash for financial reporting purposes? 1 JVCU Which of the following is considered cash for financial reporting purposes? 1
-
Required information The Foundational 15 [LO8-2, LO8-3, LO8-4, LO8-5, LO8-7, LO8-9, L08-10) (The following information applies to the questions displayed below.) Morganton Company makes one product...

Study smarter with the SolutionInn App


