A stirred tank with volume V_t?(L) is charged with V₁ (L) of a liquid. B. The space above the liquid (volume V_g = V_t ? V₁) is filled with a pure gas, A, at an initial pressure P₀ (atm). The initial system temperature is T₀ (K). The stirrer in the tank is turned on, and A begins to dissolve in B. The dissolution continues until the liquid is saturated with A at the final system temperature (T) and pressure (P). The equilibrium solubility of A in B is governed by the following expression, which relates the molar A/B ratio in the liquid to the partial pressure of A in the gas phase (which in turn equals the pressure in the tank, since the gas is pure A): r(mol A/mol B) = k_s P_A(atm) where k_s [mol A/(mol B ? atm)] = _C0 + _c1 T (K) When solving the problems to be given, use the following variable definitions:

? M_A, M_B = molecular weights of A and B

? C_vA, C_vB, C_vS?[J/ (g ? K) = constant-volume heat capacities of A(g), B(l), and solutions of A in B. respectively

? SG_B = specific gravity of B (l)

? ?U_S (J/mol A dissolved) = internal energy of solution at 298 K (independent of composition over the range of concentrations to be considered)

? n_A0, n_B0 = g-moles of A(g) and B(l) initially charged into the tank

? n_A(l) n_A(v) = g-moles of A dissolved and remaining in the gas phase at equilibrium, respectively Make the following assumptions:

? A negligible amount of B evaporates.

? The tank is adiabatic and the work input to the tank from the stirrer is negligible.

? The gas phase behaves ideally.

? The volumes of the liquid and gas phases may be considered constant.

? The heat capacities CA, Cr8, and C are constant independent of temperature and (in the case of C_vs) solution composition.

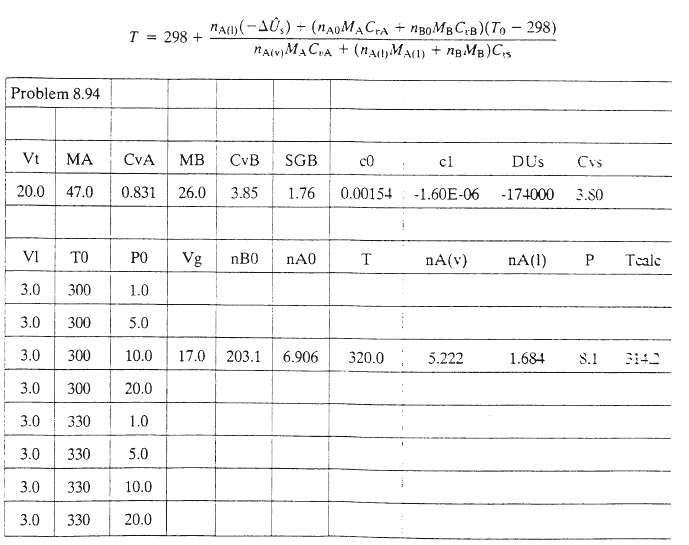
(a) Use material balances, the given equilibrium solubility relation, and the ideal gas equation of state to derive expressions for n_A0, n_B0, n_A(v),?n_A(1) and P in terms of the final temperature, T and variables M_A, M_B, SG_B, V_t, V₁, T₀. P₀, c₀, and c₁ then use an energy balance to derive the following equation:

(b) Write a spreadsheet to calculate T from specified values of M_A (47), M_B (= 26), SG_B (= 1.6) V_t (= 20.0), V₁ (= 3.0), C₀ (= 1.54 x 10^-3), C_1?(= ?1.60 x 10^-6). C_rA (= 0.831), C_rB (= 3.85) C_vs (= 3.80), and ?Us (= ?1.74 x 10⁵), and a number of different values of T₀ and P₀. The spreadsheet should have the structure given below. (Calculated values are shown for one initial temperature and pressure.) The values of V_g, n_B0, and n_A0 should first be calculated from the even values of the other variables. Next, a value of T should be guessed (in the example in the table, the 2uess.ed value is 320 K), the values of n_A(v), n?n_A(1), and P should be calculated from the equations derived in part (a), and the temperature should be recalculated from the energy balance in the column labeled T _calc (it equals 314.2 in the example). The value of T should then be varied until it equals the recalculated value of (Suggestion: Create a new cell as T ? T _calc and use goal seek to find the value of T that drives T ? T to zero.) Enter the formulas in the cells for V₁ = 3.0 L, T₀ = 300 K, and P₀ = 10.0 atm. and verify that your cell values match those shown above. Then find the correct value of T Using the procedure just described, copy the formulas into the other rows of the table, and determine T for each set of initial conditions. Summarize the effects of the initial temperature and pressure on the adiabatic temperature rise and briefly explain why your results make sense.

(c) Write a computer program to perform the same calculations done with the spreadsheet in pan (b).

? Define values of V_t, M_A, C_vA, M_B, C_vB, SG_B, _C0, _C1, ?Us, and C_vs. Use the values shown in the fourth row of the spreadsheet.

? Read in a set of values of VB, T0, and Po. Have the program terminate if V_B 0.0.

? If a positive value is read in for V_B, calculate V_G, n_B, and n_A0

? Assume a value of T. (Try 1.1 T₀ as a first guess.)

? Calculate n_A(v), n_A(1), and P from the equations derived in part (a), then recalculate T from the energy balance. Print out the values of T (assumed), P, n_A(v), n_A(1), and T (recalculated).

? If the assumed and recalculated values of T are within 0.01 K of each other, end the loop and go back to read the next set of input variables. If they are not and more than 15 iterations have been performed terminate with an error message. Otherwise, repeat the previous step using the recalculated value of T as the assumed value for this iteration. Run the program for the eight sets of conditions shown in the spreadsheet table.

Transcribed Image Text:

Problem 8.94 T = 298 + Vt RAM)(-AUS) (NAOMACA + BOMB CEB)(To - 298) RAIV) MACA (MAMA) + ng MB) C₁s MA CVA MB CvB SGB со 20.0 47.0 0.831 26.0 3.85 1.76 0.00154 VI TO 3.0 300 3.0 300 3.0 300 3.0 300 20.0 3.0 330 1.0 3.0 330 5.0 3.0 330 10.0 3.0 330 20.0 + Vg nB0 ΠΑΟ PO 1.0 5.0 10.0 17.0 203.1 6.906 320.0 T cl -1.60E-06 nA (v) 5.222 DUS Cvs -174000 3.80 nA (1) P Tcalc 1.684 S.1 3142