In Example 5.3.3, the digits are drawn to solve a replacement problem. Obtain the probability of obtaining at least two even numbers in a draw of five using the leading digits of e.

Data from in Example 5.3.3

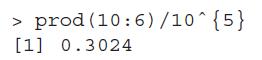
Feller (1968), pages 31–2. Consider the population of 10 digits, 0, 1, … , 9. Suppose that we draw five digits, with replacement, randomly from it and wish to compute the probability of all the five digits being different. By earlier discussion, this probability is easily seen to be p = (10)₅∕10⁵, which on evaluation gives the answer, in R, as

Feller argues this probability through the use of mathematical tables. Let us begin with his discussion on the use of digits of the irrational number e. Consider the first 800 digits of e. Thereader may obtain the first 2 million digits of e at http://apod.nasa.gov/htmltest/gifcity/e.2mil, and we too have obtained the values from it. The 800 digits can be grouped into 160 units, each unit consisting of a succession of 5 digits. Group the 160 units into 16 batches, with each batch containing 10 groups of 5 digits of the irrational number e. Finally, find the frequency of numbers in which the block has all distinct digits. We will first discuss the program for Fellers arguments.

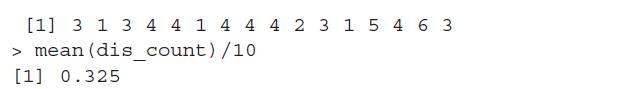
Let us understand this program. The dataset e800 consists of the first 800 digits of the irrational number e. The object dis_count represents the number of times we have unique digits among the five digits in a batch of ten such collections, and this is obtained through the loop for(j in 1:nrow(temp)). The search is carried out for all the 16 blocks in the loop for(i in 1:16). Thus, the average of dis_count returns the probability of 0.325, which is closer to the theoretical probability of 0.3024.

Transcribed Image Text:

prod (10:6)/10^{5} [1] 0.3024