In Subsection 2.4.1, we computed the norm of a vector x as sqrt (sum(x ̂ 2)). With some extra effort, it is indeed possible to obtain the same using the R function norm. Explore the options type and complete the use of the norm function which gives the same answer as sqrt(sum(x ̂ 2)).

Data from in Subsection 2.4.1

2.4.1 Vectors

We begin with some elementary properties of vectors. Let x = (x₁, x₂, · · · , x_p) and y = (y₁, y₂, · · · , y_p) be two p-dimensional vectors. The basic operations of scalar addition, multiplication, etc., are defined in the following:

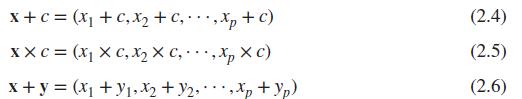
Let us first understand the vector computations in R.

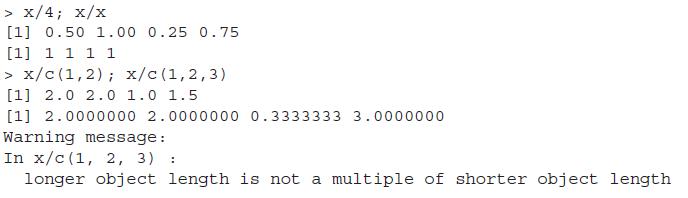
In the example of scalar addition/multiplication, the number 3 is simply added/multiplied to each element of the vector x. Addition and multiplication of two equal vectors is also performed element wise. However, when we add or multiply unequal vectors, not allowed from a pure mathematical point of view, the computations are performed in a certain defined manner. First, the lengths of both the vectors are determined, and the minimum length vector is added element wise to the larger vector and the process is repeated for the remaining length of the larger vector. If the shorter vector length is an exact integer multiple of the lengthier one, R deems it appropriate. In cases where it is not true, a warning message is released. Let us now consider the working of the division operator.

Transcribed Image Text:

x + c = (x₁ + C, X₂ + C₂, Xp + c) XXC = (x₁ X C, X₂ X C₂, Xp X c) x + y = (x₁+y₁, x₂ + y₂₂₂ Xp + p) (2.4) (2.5) (2.6)