The nerve dataset, as discussed in Section 8.2, deals with the cumulative distribution function. Estimate the density function of the nerve data using histogram smoothing, and uniform, Epanechnikov, biweight, and Gaussian kernels.

Data from in  Section 8.2

Let X₁, X₂, … , X_n be a random sample from an unknown distribution function F on the real  line. The empirical distribution function, abbreviated as edf, is then defined by

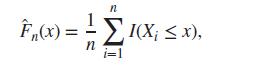
where I{} is an indicator function. The edf is very intuitive and plays a highly useful tool in non-parametric inference. The asymptotic properties of edf are best explained by the Glivenko-Cantelli theorem, sometimes called the fundamental theorem of statistics. The asymptotic and other useful properties of edf are stated next, see Chapter 2 of Wasserman (2006).

Transcribed Image Text:

n Fn() = = Στα; ≤ x), : n =1