Completing a detail of the proof of Theorem 12.5, let G be a finite group of plane isometries. Show that the rotations in G, together with the identity isometry, form a subgroup H of G, and that either H = G or |G| = 2|H|. 

Data from Theorem 12.5

Every finite group G of isometries of the plane is isomorphic to either Z₁₁ or to a dihedral group D₁₁ for some positive integer n. 

Proof: Outline First we show that there is a point P in the plane that is left fixed by every isometry in G. This can be done in the following way, using coordinates in the plane. Suppose G = {∅₁. ∅₂. · · ·. ∅_m} and let (x_i . y_i = ∅_i (0.0).

Then the point 

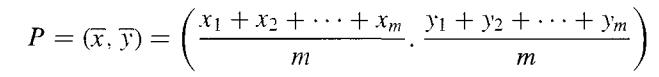
is the centroid of the set S = {(x_i. Y_i) I i = 1. 2. • • • . m}. The isometries in G permute the points in S among themselves, since if since if ∅_i ∅_j = ∅_k then ∅_i (x_j . y_j = ∅_i {∅_j (0, 0)  ∅_k(0.0) = (x_k. y_k ). It can be shown that the centroid of a set of points is uniquely determined by its distances from the points, and since each isometry in G just permutes the set S, it must leave the centroid (x̅ . y̅ )fixed. Thus G consists of the identity, rotations about P, and reflections across a line through P.

The orientation-preserving isometries in G form a subgroup H of G which is either all of G or of order m /2. This can be shown in the same way that we showed that the even permutations are a subgroup of S_n containing just half the elements of S_n •Of course H consists of the identity and the rotations in G. If we choose a rotation in G that rotates the plane through as small an angle Θ > 0 as possible, it can be shown to generate the subgroup H. (See Exercise 23.) This shows that if H = G, then G is cyclic of order m and thus isomorphic to Z_m. Suppose H ≠ G so that G contains some reflections. Let H = {i, P₁, · • · , P_n-1 with n = m /2. If µ is a reflection in G, then the coset H µ consists of all n of the reflections in G. 

Consider now a regular n-gon in the plane having P as its center and with a vertex lying on the line through P left fixed by µ. The elements of H rotate this n-gon through all positions, and the elements of H µ first reflect in an axis through a vertex, effectively turning the n-gon over, and then rotate through all positions. Thus the action of G on this n-gon is the action of D_n, so G is isomorphic to D_n.

Transcribed Image Text:

P = (x, y) = x₁ + x₂ + m .. . +xm 1 + ¹2 + ·· ... m + Y'm