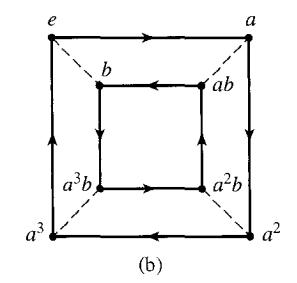
Consider Cayley digraphs with two arc types, a solid one with an arrow and a dashed one with no arrow, and consisting of two regular n-gons, for n ≥ 3, with solid arc sides, one inside the other, with dashed arcs joining the vertices of the outer n-gon to the inner one. Figure 7 .9(b) shows such a Cayley digraph with n = 3, and Figure 7.ll(b) shows one with n = 4. The arrows on the outer n-gon may have the same (clockwise or counterclockwise) direction as those on the inner n-gon, or they may have the opposite direction. Let G be a group with such a Cayley digraph.

a. Under what circumstances will G be abelian? 

b. If G is abelian, to what familiar group is it isomorphic? 

c. If G is abelian, under what circumstances is it cyclic? 

d. If G is not abelian, to what group we have discussed is it isomorphic?

Figure 7.9 b

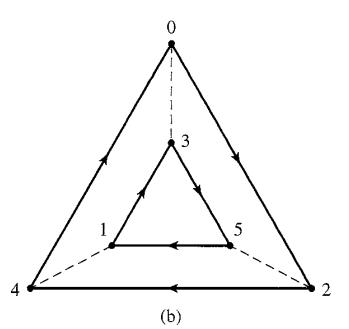
Figure 7.11b

4 0 3 (b) 5 2