Give a one- or two-sentence synopsis of the proof of Theorem 31.4. 

Data from Theorem 31.4

If E is a finite extension field of a field F, and K is a finite extension field of E, then K is a finite extension of F, and [K : F] = [K : E][E : F]

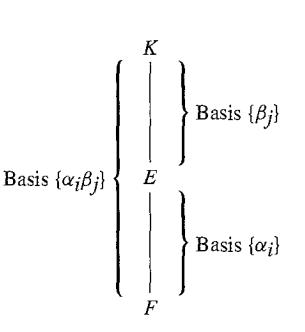
Proof Let {α_i | i = 1, ··· , n} be a basis for E as a vector space over F, and let the set {β_j | j = 1, ···, m} be a basis for K as a vector space over E. The theorem will be proved if we can show that the mn elements α_i ,β_j  form a basis for K, viewed as a vector space over F. Let γ be any element of K. Since the β_j form a basis for K over E, we have 

for bj ∈ E. Since the α_i form a basis for E over F, we have

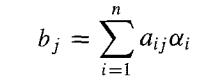
for a_ij ∈ F. Then

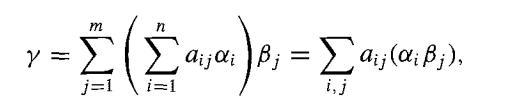
so the mn vectors α_iβ_j span K over F. It remains for us to show that the mn elements α_iβ_j are independent over F. Suppose that ∑_i,j c_ij (α_iβ_j) = 0, with C_ij ∈ F. Then

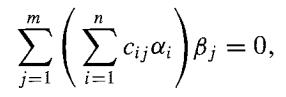
and ∑_iⁿ₌₁c_ij (α_i)  ∈ E. Since the elements β_j are independent over E, we must have

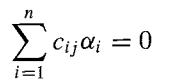
for all j. But now the α_i are independent over F, so  ∑_iⁿ₌₁c_ijα_i = 0 implies that C_ij = 0 for all i and j. Thus the α_iβ_j not only span K over F but also are independent over F. Thus they form a basis for K over F.

Transcribed Image Text:

Basis {ij} K E F Basis {j} Basis {a}