In using the three isomorphism theorems, it is often necessary to know the actual correspondence given by the isomorphism and not just the fact that the groups are isomorphic. 

In the group G = Z₂₄, let H = (4) and K = (8). 

a. List the cosets in G/H, showing the elements in each coset. 

b. List the cosets in G/K, showing the elements in each coset. 

c. List the cosets in H/K, showing the elements in each coset. 

d. List the cosets in (G/K)/(H/K), showing the elements in each coset. 

e. Give the correspondence between G/ Hand (G/K)/(H/K) described in the proof of Theorem 34.7.

Data from Theorem 34.9

Let H and K be normal subgroups of a group G with K ≤ H. Then G/H ≈ (G/K)/(H/K). 

Proof Let ∅ : G → (G/K)/(H/K) be given by ∅(a)= (aK)(H/K) for a ∈ G. Clearly ∅ is onto (G/K)/(H/K), and for a, b ∈ G, 

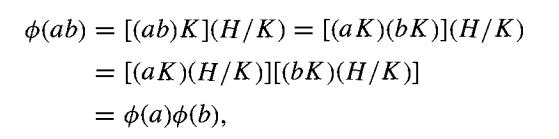
so ∅ is a homomorphism. The kernel consists of those x ∈ G such that ∅(x) = H/K. These x are just the elements of H. Then Theorem 34.2 shows that G/H ≈ (G/K)/(H/K).

Transcribed Image Text:

p(ab) = [(ab)K](H/K) = [(aK)(bK)](H/K) = [(aK)(H/K)][(bK)(H/K)] = φ(α)φ(b),