Question: It is a fact, which we can verify by cubing, that the zeros of x 3 - 2 in Q are where 3 2, as

It is a fact, which we can verify by cubing, that the zeros of x3 - 2 in Q are

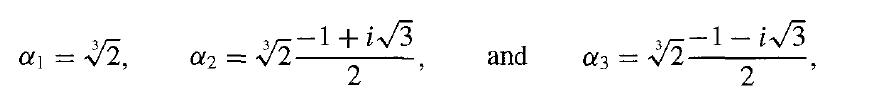
a = 32, -1+i3 2 / = 3/2= and 3 = 32.


where 3√2, as usual, is the real cube root of 2.

Describe all extensions of the automorphism ψ√3,-√3 of Q(√3) to an isomorphism mapping Q(i, √3, 3√2) onto a subfield of Q̅.

a = 32, -1+i3 2 / = 3/2= and 3 = 32. . -1-i3 2

Step by Step Solution

★★★★★

3.39 Rating (152 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

The extensions are T given by 7 i i T2 giv... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related A First Course In Abstract Algebra Questions!

Q:

It is a fact, which we can verify by cubing, that the zeros of x 3 - 2 in Q are where 3 2, as usual, is the real cube root of 2. Describe all extensions of the identity map of Q to an isomorphism...

Q:

It is a fact, which we can verify by cubing, that the zeros of x 3 - 2 in Q are where 3 2, as usual, is the real cube root of 2. Describe all extensions of the identity map of Q to an isomorphism...

Q:

It is a fact that 513,239 x 194,841 = 0.18181818... Using the preceding multiplication fact to find the exact decimal representations of 1/513,239 and 1/194,841. If the decimal representation is...

Q:

\fCOMPLEX VARIABLES AND APPLICATIONS Eighth Edition James Ward Brown Professor of Mathematics The University of Michigan-Dearborn Ruel V. Churchill Late Professor of Mathematics The University of...

Q:

\fCOMPLEX VARIABLES AND APPLICATIONS Eighth Edition James Ward Brown Professor of Mathematics The University of Michigan-Dearborn Ruel V. Churchill Late Professor of Mathematics The University of...

Q:

Referring to Example 50.9, show that G(Q( 3 2, i3)/Q(i3)) (Z 3 , +). Data from in Example 50.9 - Let 2 be the real cube root of 2, as usual. Now x 2 does not split in Q(V2), for Q(2)

Q:

Refer to Example 50.9 What is the order of G(Q( 3 2, i3)/Q( 3 2))? Data from in Example 50.9 - Let 2 be the real cube root of 2, as usual. Now x 2 does not split in Q(V2), for Q(2)

Q:

Refer to Example 50.9 What is the order of G(Q( 3 2, i3)/Q)? Data from in Example 50.9 - Let 2 be the real cube root of 2, as usual. Now x 2 does not split in Q(V2), for Q(2)

Q:

Let K be the splitting field of x 3 - 2 over Q. a. Describe the six elements of G(K/Q) by giving their values on 3 2 and i3. (By Example 50.9, K = Q( 3 2, i 3).) b. To what group we have seen before...

Q:

All the information are in it (i) g(x) = x?(x + 5)%(x 1)(x 4) (a) Degree: ; Leading coefficient: ; based on this the end behavior is: (b) the x-intercepts: X-intercept Multiplicity Bounce or cross?...

Q:

A certain health maintenance organization (HMO) is studying its daily office routine. They collect information on three variables: the number of patients who visit during a day, the patients...

Q:

A firm plans to issue $400,000 in 45 day commercial paper. If the firm can sell commercial paper for 390,000. What is the effective annual rate for the commercial paper? assume a 365 day year?

Q:

3.77 Have you wondered how Internet connection speed varies around the globe? The file Connection Speed contains the mean connection speed, the mean peak connection speed, the percentage of the time...

Q:

explain the process of using confrontation, and

Q:

Reconsider the previous exercise about the effect of social media on a persons self-esteem. In the actual study conducted by the statistics students, there were 27 people assigned to each of the...

Q:

Reconsider the previous exercise about the effect of social media on a persons self-esteem. In the actual study conducted by the statistics students, participants were given a score that measured...

Q:

Students in a statistics class in a four-year university in California were randomly assigned to be asked one of the following three questions: Suppose that a part of the state of California was...

Q:

Which of the following may indicate liquidity problems in high sales growth companies earlier than other liquidity ratios? Net sales to working capital Current ratio Quick ratio Short - term debt to...

Q:

Please solve in excel or word. roblem 3 A) Suppose that the following holds: (1+fn,n+k)k(1+YTMn)n>(1+YTMn+k)n+k, where fn,n+k is the forward rate from period n up to period n+k,YnMn is the...

Q:

Please include all necessary formulas. Thank you! Problem 9.4: R \& J, Inc. issues a 10-year $1,000 bond that pays $28.50 semi-annually. The market price for the bond is $975. The market's required...