Let be a primitive 5th root of unity in C. a. Show that Q() is the

Let ζ be a primitive 5th root of unity in C.

a. Show that Q(ζ) is the splitting field of x⁵ - 1 over Q.

b. Show that every automorphism of K
= Q(ζ) maps ζ onto some power ζ^r of ζ. 

c. Using part (b), describe the elements of G(K/Q).

d. Give the group and field diagrams for Q(ζ) over Q, computing the intermediate fields as we did in Examples 54.3 and 54.7.

Data from in 54.7 Example 

Consider the splitting field of x⁴ + 1 over Q. By Theorem 23.11, we can show that x⁴ + 1 is irreducible over Q, by arguing that it does not factor in Z[x]. (See Exercise 1.) The work on complex number in Section 1 shows that the zeros of x⁴ +1 are (1 ± i)/√2 and (-1 + i)/√2. A computation shows that if

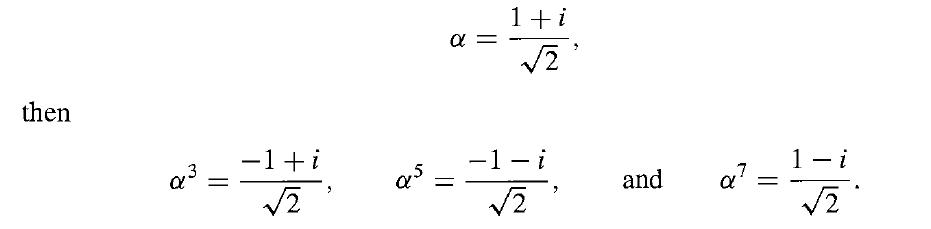
Thus the splitting field K of x⁴ + 1 over Q is Q(α), and [K : Q] = 4. Let us compute G(K/Q) and give the group and field diagrams. Since there exist automorphisms of K mapping α onto each conjugate of α, and since an automorphism σ of Q(α) is completely determined by σ(α), we see that the four elements of G(K/Q) are defined by Table 54.8. Since (σ_jσ_k)(α) = σ_j(α^k) = (α^j)^k = a^jk and α⁸ = 1, we see that G(K/Q) is isomorphic to the group {1, 3, 5, 7} under multiplication modulo 8. This is the group G₈ of Theorem. 20.6. Since σ²_j = σ₁, the identity, for all j, G(K/Q) must be isomorphic to the Klein 4-group. The diagrams are given in Fig. 54.9.

Transcribed Image Text:

then Q³ −1+i √2 a5 α || - 1 + i √2 1- i √2 > and a² = 1- i √2