Let R = {a + b2 | a, b Z} and let R' consist of all
Question:
Let R = {a + b√2 | a, b ∈ Z} and let R' consist of all 2 x 2 matrices of the form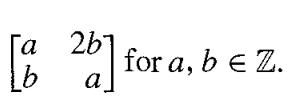
Show that R is a subring of !R. and that R' is a subring of M2(Z). Then show that ∅ : R → R', where ∅(a + b√2) =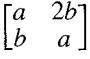
ls an isomorphism.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Because a b2c d2 a cb d 2 and 0 0 02 and a b2 ab2 we see tha...View the full answer
Answered By
Aysha Ali
my name is ayesha ali. i have done my matriculation in science topics with a+ . then i got admission in the field of computer science and technology in punjab college, lahore. i have passed my final examination of college with a+ also. after that, i got admission in the biggest university of pakistan which is university of the punjab. i am studying business and information technology in my university. i always stand first in my class. i am very brilliant client. my experts always appreciate my work. my projects are very popular in my university because i always complete my work with extreme devotion. i have a great knowledge about all major science topics. science topics always remain my favorite topics. i am also a home expert. i teach many clients at my home ranging from pre-school level to university level. my clients always show excellent result. i am expert in writing essays, reports, speeches, researches and all type of projects. i also have a vast knowledge about business, marketing, cost accounting and finance. i am also expert in making presentations on powerpoint and microsoft word. if you need any sort of help in any topic, please dont hesitate to consult with me. i will provide you the best work at a very reasonable price. i am quality oriented and i have 5 year experience in the following field.
matriculation in science topics; inter in computer science; bachelors in business and information technology
_embed src=http://www.clocklink.com/clocks/0018-orange.swf?timezone=usa_albany& width=200 height=200 wmode=transparent type=application/x-shockwave-flash_
11+ Reviews
14+ Question Solved
Related Book For 
Question Posted:
