Let V and V' be vector spaces over the same field F. A function ∅ : V → V' is a linear transformation of V into V' if the following conditions are satisfied for all α, β ∈ V and a ∈ F:

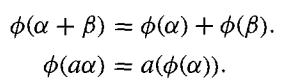
a. If {β_i | i ∈ I} is a basis for V over F, show that a linear transformation ∅ : V → V' is completely determined by the vectors ∅(β_i) ∈ V'.

b. Let {β_i | i ∈ I} be a basis for V, and let {β_i'| i ∈ I} be any set of vectors, not necessarily distinct, of V'. Show that there exists exactly one linear transformation ∅ : V → V' such that ∅(β_i)= β_i'.

Transcribed Image Text:

φ(α + β) = φ(α) + φ(β). φ(αα) = α(φ(α)).