Referring to Exercise 27, find all subgroups of S 3 (Example 8.7) that are conjugate to {P
Question:
Referring to Exercise 27, find all subgroups of S3 (Example 8.7) that are conjugate to {P0, µ2}.
Data from Exercise 27
A subgroup H is conjugate to a subgroup K of a group G if there exists an inner automorphism ig of G such that ig[H] = K. Show that conjugacy is an equivalence relation on the collection of subgroups of G.
Data from Example 8.7.
An interesting example for us is the group S3 of3! = 6 elements. Let the set A be {1, 2, 3}. We list the permutations of A and assign to each a subscripted Greek letter for a name.
The reasons for the choice of names will be clear later. Let
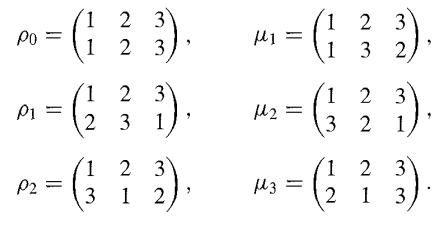
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





