(a) Laguerre’s differential equation

ty'' + (1 - t)y' + ny = 0

is known to possess polynomial solutions when n is a nonnegative integer. These solutions are naturally called Laguerre polynomials and are denoted by Ln(t). Find y = Ln(t), for n = 0, 1, 2, 3, 4 if it is known that L_n(0) = 1.

(b) Show that

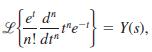
Where Y(s) = ℒ{y} and y = L_n(t) is a polynomial solution of the DE in part (a). Conclude that

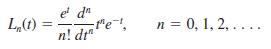
This last relation for generating the Laguerre polynomials is the analogue of Rodrigues’ formula for the Legendre polynomials. See (33) in Section 6.4.

Transcribed Image Text:

[e' d" n! dr = Y(s),