A matrix A is said to be nilpotent if there exists some positive integer m such that
Question:
A matrix A is said to be nilpotent if there exists some positive integer m such that Am = 0. Verify that
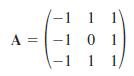
is nilpotent. Discuss why it is relatively easy to compute eAt when A is nilpotent. Compute eAt and then use (1) to solve the system X' = AX.
Transcribed Image Text:
-1 1 -1 0 -1 1 A = 1
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Answer rating: 41% (12 reviews)
Verify that A is nilpotent Therefore A m A 3 0 ie m3 15 Nilpotent Now ...View the full answer

Answered By

Santosh Rathod
I comleted bachelor degree in engineering ( electronics and telecommutication )form the govt college of engineering jalgaon with first class 65 % in 2013 and after comleted graduate and in graduate i intrested in solving mathematics questions of variese exames.
I have about 6 years of teaching/tutoring experience. I have taught a range of subjects that I have an academic background in or even languages that I speak. One of the best ways to gain teaching experience is to teach someone for free or in exchange for them teaching you.
I tutored mostly elementary school students privately after school and during the summer. We met in their homes or at the public library. I charged an hourly fee, and I provided any necessary materials.
0.00
0 Reviews
10+ Question Solved
Related Book For 

A First Course in Differential Equations with Modeling Applications
ISBN: 978-1111827052
10th edition
Authors: Dennis G. Zill
Question Posted:
Students also viewed these Mathematics questions
-
A n n matrix is said to be nilpotent if Ak = 0 for some positive integer k. Show that all eigen values of a nilpotent matrix are 0.
-
A matrix B is said to be a square root of a matrix A if BB = A. (a) Find two square roots of (b) How many different square roots can you find of (c) Do you think that every 2 Ã 2 matrix has at...
-
When a pure substance is placed in contact with water, there are three possible outcomes. The substance may do nothing that is, the substance does not dissolve and no visible change takes place. The...
-
Find the exact value of sin(x - y) if sin(x) = 3T 3T T
-
An Internet book retailer promises to ship all customer orders within 24 to 36 hours of receiving an order at its web site. Actual shipment data for all computers shipped during the past month showed...
-
What arguments would you use to persuade a team of managers of the need to listen to the views of staff and to take them seriously?? L01
-
Calculate the MHR for Machine A from the following data: Cost of machine Rs 1,600 Estimated scrap value Rs 100 Effective working life 10,000 hours Running time per 4 weekly period 160 hours Average...
-
Stabler Co.s projected March 31, 2011, balance sheet follows. Additional information about the company is as follows: ¢ Expected sales for April and May are $240,000 and $260,000, respectively....
-
4 of 15 3 complete) HW Score: 10%, 10 of 1 X ED-18 (similar to) The financial statements of Vanna's Natural Foods include the folowing for Od the con to view the financial statements.) Financial...
-
Langdale Ltd is a small company manufacturing and selling two different products the Lang and the Dale. Each product passes through two separate production cost centres a machining department,...
-
In problem use variation of parameters to solve the given system. X' = (: X + 0, -1 sec t tan t,
-
(a) Use (1) to find the general solution of Use a CAS to find e At . Then use the computer to find eigenvalues and eigenvectors of the coefficient matrix and form the general solution in the manner...
-
Paul Keller tripped the sequence switches at control monitor 23 in accordance with the countdown instruction just to his left. All hydraulic systems were functioning normally in the second stage of...
-
Stefney Christian Date: 06/26/2023 To: From: New England Patriot Subject: Analysis of Aircraft Purchase vs. Chartering Decision I've done a thorough analysis of the decision to buy or charter a plane...
-
The Giovonis' monthly income is $9000. The have 14 remaining payments of $269 on a new car and 16 payments of $70 remaining on their living room furniture. The taxes and insurance on the house are...
-
2. Determine the following inverse z-transforms using partial fraction expansion method. a. The sequence is right sided (causal). 1 z 14z 2 + 4z-3 X(z) = 11 1 Z-1 13 + 2-2 8 1 -3 4Z b. The sequence...
-
(4 pts) 1. Find all vertical and horizontal asymptotes of the function f(x) (You do NOT need to show the limit work) 2x2-2 x+4x+3
-
Cherboneau Novelties produces drink coasters (among many other products). During the current year (year 0), the company sold 532,000 units (packages of 6 coasters). In the coming year (year 1), the...
-
Quinn Company reported a net deferred tax asset of $6,300 in its December 31, 20X0, balance sheet. For 20X1, Quinn reported pre-tax financial statement income of $300,000. Temporary differences of...
-
The figure shows a bolted lap joint that uses SAE grade 8 bolts. The members are made of cold-drawn AISI 1040 steel. Find the safe tensile shear load F that can be applied to this connection if the...
-
Suppose we regard a preparation as being bioavailable for a subject at the first week when level of plasma carotene increases by 50% from the baseline level (based on an average of the first and...
-
Assess whether there are significant differences among the survival curves obtained in Problem 14.12?
-
Answer the same question as in Problem 14.12 assuming the criterion for bioavailability is a 100% increase in plasma-carotene level from baseline?
-
Yard Professionals Incorporated experienced the following events in Year 1, its first year of operation: Performed services for $31,000 cash. Purchased $7,800 of supplies on account. A physical count...
-
This question is from case # 24 of book Gapenski's Cases in Healthcare Finance, Sixth Edition Select five financial and five operating Key Performance Indicators (KPIs) to be presented at future...
-
assume that we have only two following risk assets (stock 1&2) in the market. stock 1 - E(r) = 20%, std 20% stock 2- E(r) = 10%, std 20% the correlation coefficient between stock 1 and 2 is 0. and...

Study smarter with the SolutionInn App


