(a) Reread Problem 8 of Exercises 3.3. In that problem you were asked to show that the system of differential equations

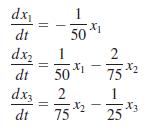
is a model for the amounts of salt in the connected mixing tanks A, B, and C shown in Figure 3.3.7. Solve the system subject to x₁(0) = 15, x₂(t) = 10, x³(t) = 5.

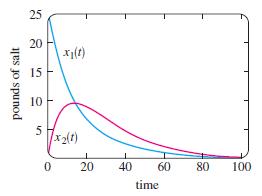
(b) Use a CAS to graph x₁(t), x₂(t), and x₃(t) in the same coordinate plane (as in Figure 4.9.1) on the interval [0, 200].

(c) Because only pure water is pumped into Tank A, it stands to reason that the salt will eventually be flushed out of all three tanks. Use a root-finding application of a CAS to determine the time when the amount of salt in each tank is less than or equal to 0.5 pound. When will the amounts of salt x₁(t), x₂(t), and x₃(t) be simultaneously less than or equal to 0.5 pound?

Problem 8 of Exercises 3.3.

Three large tanks contain brine, as shown in Figure 3.3.7. Use the information in the figure to construct a mathematical model for the number of pounds of salt x₁(t), x₂(t), and x₃(t) at time t in tanks A, B, and C, respectively. Without solving the system, predict limiting values of x₁(t), x₂(t), and x₃(t) as t → ∞.

Figure 3.3.7.

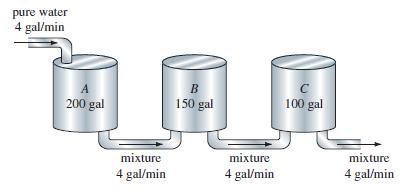
Figure 4.9.1

Transcribed Image Text:

dx, dt 501 dx2 1 dt 50 75 dx, 1 X2 75 dt 25