(a) The differential equation x 4 y ' ' y 0 has an irregular singular point at x 0 Show that the substitution t 1 x yields the DE which now has a regular singular point at t 0 (b) Use the method of this section to find two series solutions of the second equation in part (a) about the regular singul...

The Answer is in the image, click to view ...

(a) The differential equation x 4 y'' + y = 0 has an irregular singular point at...

Question:

(a) The differential equation x⁴y'' + λy = 0 has an irregular singular point at x = 0. Show that the substitution t = 1 x yields the DE

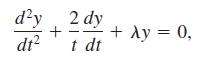
d'y, 2 dy + Ay = 0, + dt? t dt

which now has a regular singular point at t = 0.

(b) Use the method of this section to find two series solutions of the second equation in part (a) about the regular singular point t = 0.

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

A First Course in Differential Equations with Modeling Applications

ISBN: 978-1111827052

10th edition

Authors: Dennis G. Zill

See More Books

Question Posted: Oct 29, 2020 08:53 AM

See More Questions

Each of the differential equations x 3 y'' + y = 0 and x 2 y'' + (3x 1)y' + y = 0 has an irregular singular point at x = 0. Determine whether the method of Frobenius yields a series solution of each...
A regular singular point at x = 1 and an irregular singular point at x = 0 In problem construct a linear second-order differential equation that has the given properties.
Express p (x) = 1 + 2x - 5x2 as a Taylor polynomial about a = 1. In calculus, you learn that a Taylor polynomial of degree n about a is a polynomial of the form p(x) = a0 + a1(x - a) + a2(x - a)2 + ...
Peete's Coffee and Tea purchased equipment on March 1, 2022 for $17,400. It is estimated that the equipment will have a $300 salvage value at the end of its 6 -year useful life. It is also estimated...
Let f : (0; 1) R be bounded but such that does not exist. Show that there are two sequences (xn) and (yn) in (0, 1) with lim(xn) = 0 = lim(yn), but such that (f(xn)) and (f(yn)) exist but are not...
What are your thoughts on Checkpoint? What are its strengths and potential limitations? Would you like to be evaluated with a system such as this?
When certain charges are paid by the company or agency and the rest are to be borne by the guest himself, the split is made on the basis of charges. The bill in such a case is called_______ bill.
Arthur Andersen LLP was the auditor for Enron, WorldCom, Waste Management and other companies that committed fraud. Andersen was forced to shut its doors forever after a U.S. Department of Justice...
Submission Week-10 The motherboard manufacturing activities of Luboh P/L includes the following relevant cost | drivers and allocation bases. Based on past experience cost rates for the given...
Consider the ammonia Rankine-cycle power plant shown in, a plant that was designed to operate in a location where the ocean water temperature is 25C near the surface and 5C at some greater depth. a....
Verify by direct substitution that the given power series is a solution of the indicated differential equation. For a power x 2n+1 let k = n + 1. y = x", (x + 1)y" + y' = 0 n n=1
Use the change of variables to show that the differential equation of the aging spring mx'' + ke -at x = 0, = > 0, becomes 2 -at/2 V m
Which of the following is a disadvantage of outsourcing? A. Freeing up capacity B. Freeing up capital C. Transferring production and technology risks D. Limiting ability to upsize or downsize...
Write a brief statement that interprets the confidence interval. Choose the correct answer below. A. There is a 99% chance that the true value of the population mean weight of newborn girls will fall...
Transcribed image text: If estimated annual factory overhead is $1,072,500; overhead is applied using direct labor hours, estimated annual direct labor hours are 275,000 actum March factory overhead...
Your firm has limited capital to invest and is therefore interested in comparing projects based on the profitability index (PI), as well as other measures. What is the PI of the project with the...
The following rates are applicable to annual payroll in British Columbia Question 17 options: 1234 1.95% x total B.C. remuneration 1234 2.925% x (B.C. remuneration - $500,000) 1234 Tax Rate 1234...
Assume that different groups of couples use a particular method of gender selection and each couple gives birth to one baby. This method is designed to increase the likelihood that each baby will be...
The Trafford Corporation needs to raise $60 million to finance its expansion into new markets. The company will sell new shares of equity via a general cash offering to raise the needed funds. If the...
A heat engine has a heat input of 3 Ã 104 Btu/h and a thermal efficiency of 40 percent. Calculate the power it will produce, in hp. Source 3 x 10 Btu/h 40% HE Sink
What is the conditional probability that the woman will be affected given that the man is affected? How does this value compare with the prevalence in Table 3.5? Why should it be the same (or...
What is the probability that at least one member of the couple is affected? Suppose the probability that both members of a married couple, each of whom is 7579 years of age, will have Alzheimers...
What is the expected overall prevalence of Alzheimers disease in the community if the prevalence estimates in Table 3.5 for specific agegender groups hold? Suppose a study of Alzheimers disease is...
Create a Data Table to depict the future value when you vary the interest rate and the investment amount. Use the following assumptions: Interest Rates: Investment Amounts:-10.0% $10,000.00 -8.0%...
Isaac earns a base salary of $1250 per month and a graduated commission of 0.4% on the first $100,000 of sales, and 0.5% on sales over $100,000. Last month, Isaac's gross salary was $2025. What were...
Calculate the price, including both GST and PST, that an individual will pay for a car sold for $26,995.00 in Manitoba. (Assume GST = 5% and PST = 8%) a$29,154.60 b$30,234.40 c$30,504.35 d$28,334.75...

(a) The differential equation x 4 y'' + y = 0 has an irregular singular point at...

Question:

d'y, 2 dy + Ay = 0, + dt? t dt

Step by Step Answer:

A First Course in Differential Equations with Modeling Applications

Students also viewed these Mathematics questions