The first-order differential equation dy/dx = x 2 + y 2 cannot be solved in terms of
Question:
The first-order differential equation dy/dx = x2 + y2 cannot be solved in terms of elementary functions. However, a solution can be expressed in terms of Bessel functions.
(a) Show that the substitution y = -1/u du/dx leads to the equation u'' + x2u = 0.
(b) Use (18) in Section 6.4 to find the general solution of u'' + x2u = 0.
(c) Use (20) and (21) in Section 6.4 in the forms
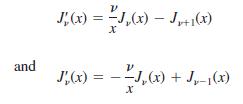
as an aid to show that a one-parameter family of solutions of dy/dx = x2 + y2 is given by
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
ANSWER a To show that the substitution y 1u dudx leads to the equation u x2u 0 we need to differenti...View the full answer
Answered By
Ragul r
I am highly experienced and dedicated educator with a passion for teaching students of all ages. With over
4 years of experience in education and tutoring, I have helped countless students achieve their academic goals in subjects such as math and science.
My journey in education began with a Bachelor's degree in from Maseno University, where I developed a strong foundation in critical thinking and problem-solving skills that have proved invaluable in my teaching career.
I am committed in helping your students in IT and various topics in sciences and math
0 Reviews
10+ Question Solved
Related Book For 
A First Course in Differential Equations with Modeling Applications
ISBN: 978-1111827052
10th edition
Authors: Dennis G. Zill
Question Posted:
