When the magnitude of tension T is not constant, then a model for the deflection curve or shape y(x) assumed by a rotating string is given by

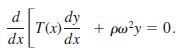
Suppose that 1 < x < e and that T(x) = x².

(a) If y(1) = 0, y(e) = 0, and ρω² > 0.25, show that the critical speeds of angular rotation are

ω_n = ½ √(4n²π² + 1)/ρ and the corresponding deflections are

yn(x) = c₂x^-1/2 sin(nπ ln x), n = 1, 2, 3, …

(b) Use a graphing utility to graph the deflection curves on the interval [1, e] for n = 1, 2, 3. Choose c₂ = 1.

Transcribed Image Text:

d dy dx + pw?y = 0. dx