In forming the Koch snowflake in Fig., the perimeter becomes greater at each step in the process. If each side of the original triangle is 1 unit, a general formula for the perimeter, L, of the snowflake at any step, n, may be determined by the formula

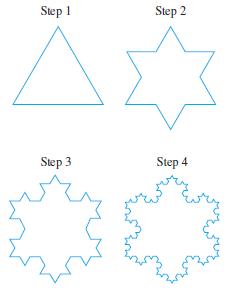
L = 3(4/3)^n-1

For example, at the first step when n = 1, the perimeter is 3 units, which can be verified by the formula as follows:

L = 3(4/3)^1-1 = 3(4/3)⁰ = 3 · 1 = 3

At the second step, when n = 2, we determine the perimeter as follows:

L = 3(4/3)^2-1 = 3(4/3) = 4

Thus, at the second step the perimeter of the snowflake is 4 units.

a) Use the formula to complete the following table.*

Step. . . . . . . . . . .Perimeter
1
2
3
4
5
6

b) Use the results of your calculations to explain why the perimeter of the Koch snowflake is infinite.

c) Explain how the Koch snowflake can have an infinite perimeter, but a finite area.

Transcribed Image Text:

Step 1 Step 2 Step 3 Step 4