A necessary and sufficient condition for positive definiteness of a quadratic form Q(x) = x T Ax
Question:
A necessary and sufficient condition for positive definiteness of a quadratic form Q(x) = xTAx with symmetric matrix A is that all the principal minors are positive that is,
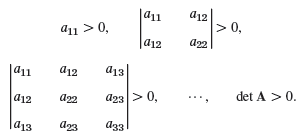
Show that the form in Prob. 22 is positive definite, whereas that in Prob. 23 is indefinite.
Data from Prob. 22
4x12 + 12x1x2 + 13x22 = 16
Data from Prob. 23
-11x12 + 84x1x2 + 24x22 = 156
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
ANSWER To determine if a quadratic form Qx xTAx is positive definite we need to check whether all th...View the full answer
Answered By
Chandrasekhar Karri
I have tutored students in accounting at the high school and college levels. I have developed strong teaching methods, which allow me to effectively explain complex accounting concepts to students. Additionally, I am committed to helping students reach their academic goals and providing them with the necessary tools to succeed.
0 Reviews
10+ Question Solved
Related Book For 
Question Posted:
