A quadratic form Q(x) = x^TAx and its (symmetric!) matrix A are called (a) positive definite If Q(x) > 0 for all x ‰  0, (b) negative definite If Q(x) < 0 for all x ‰  0, (c) indefinite If Q(x) takes both positive and negative values. (See Fig. 162.) [Q(x) and A are called positive semi definite (negative semi definite) if Q(x) ‰¥ 0 (Q(x) ‰¤ 0) for all x.] Show that a necessary and sufficient condition for (a), (b), and (c) is that the eigenvalues of A are

(a) All positive

(b) All negative

(c) Both positive and negative.

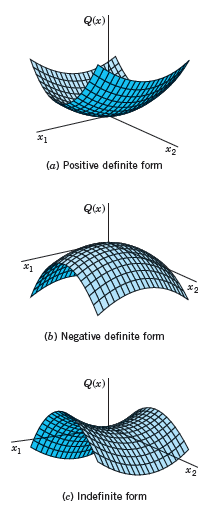Fig. 162 

Transcribed Image Text:

(a) Positive definite form Qx)| (b) Negative definite form Qx)| X1 (c) Indefinite form