A Riccati equation is of the form?

?y' + p(x)y = g(x)y² + h(x)

A Clairaut equation is of the form

y = xy' + g(y').

(a) Apply the transformation y = Y + 1/u to the Riccati equation (14), where Y is a solution of (14), and obtain for u the linear ODE u' + (2Yg - p)u = -g. Explain the effect of the transformation by writing it as y = Y + v, v = 1/u.

(b) Show that y = Y = x is a solution of the ODE y' - (2x³ + 1) y = -x²y² - x⁴ - x + 1 and solve this Riccati equation, showing the details.

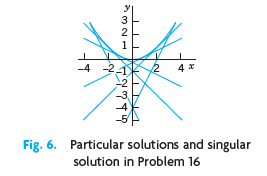
(c) Solve the Clairaut equation y^'2 - xy' + y = 0 as follows. Differentiate it with respect to x, obtaining y''(2y' - x) = 0. Then solve (A) y'' = 0 and (B) 2y' - x = 0 separately and substitute the two solutions (a) and (b) of (A) and (B) into the given ODE. Thus obtain (a) a general solution (straight lines) and (b) a parabola for which those lines (a) are tangents (Fig. 6 in Prob. Set 1.1); so (b) is the envelope of (a). Such a solution (b) that cannot be obtained from a general solution is called a singular solution.

Transcribed Image Text:

-4 -2 2 4 * -3, -5 Fig. 6. Particular solutions and singular solution in Problem 16 *321