By the principles used in modeling the string it can be shown that small free vertical vibrations of a uniform elastic beam (Fig. 292) are modeled by the fourth-order PDE

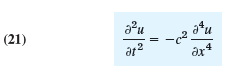
where c² = EI/ρA (E = Young’s modulus of elasticity, I = moment of intertia of the cross section with respect to the y-axis in the figure, ρ = density, A = cross-sectional area).

Find the solution of (21) that satisfies the conditions in Prob. 16 as well as the initial condition

u (x, 0) = f (x) = x(L - x).

Data from Prob. 16

By the principles used in modeling the string it can be shown that small free vertical vibrations of a uniform elastic beam (Fig. 292) are modeled by the fourth-order PDE

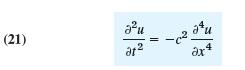
where c² = EI/ρA (E = Young’s modulus of elasticity, I = moment of intertia of the cross section with respect to the y-axis in the figure, ρ = density, A = cross-sectional area).

Find solutions u_n = F_n(x)G_n(t) of (21) corresponding to zero initial velocity and satisfying the boundary conditions (see Fig. 293A)

u (0, t) = 0, u (L, t) = 0(ends simply supported for all times t),u_xx = (0, t) = 0, u_xx (L, t) = 0(zero moments, hence zero curvature, at the ends).

(21) a2u at = ar'